Overview 概述
本文將通過兩個故事,主要講述看漲期權與看跌期權及其基本應用。
Report 報告
1636 年鬱金香狂熱
1636 年歐洲的鬱金香熱是一個經典的經濟學和金融學案例研究,在這個案例中,需求激增導致單一商品飆升到荒謬的價格。價格的飆升開啟了有記錄以來的首次大規模期權交易。
17 世紀,從土耳其和荷蘭進口到歐洲的鬱金香迅速成為富裕和美麗的象徵。當時,鬱金香就像設計師的衣服和手錶,社會各階層的人都想要。由於對鬱金香的巨大需求,種植者和經銷商對鬱金香球莖的需求也成倍增長,推高了生產者的價格。由於鬱金香球莖的價格幾乎每天都在上漲,當時最大的鬱金香球莖生產國荷蘭的經銷商開始進行鬱金香球莖期權交易,交易者只需支付一定的期權費,就可以提前擁有購買鬱金香球莖的權利,並確保一個確定的買入價格。
這就是一個鬱金香球莖的看漲期權。從1636 年底到1637 年2 月,鬱金香球莖的價格一路飆升,原本是對沖生產者風險的一種方式變成了投機狂潮。對鬱金香球莖的大量投機興趣導致社會各階層的人們即使出售或抵押他們的房子也要傾盡所有購買這些鬱金香球莖。
「所有暴力的歡愉都將迎來暴力的終結」。最終,所有的價格泡沫都破裂了。 1637 年2 月,鬱金香球莖的價格漲得如此太高,以至於它再也找不到理智的買主來出售。搶購狂潮立即變成了拋售狂潮。鬱金香球莖價格下跌的速度比上漲的速度要快,幾乎所有的期權投機者都因為鬱金香跌穿了期權的價格,變得一文不值而被掃地出門。荷蘭經濟崩潰,人們失去了他們的錢和房子。由於許多期權投機者在鬱金香熱潮中被掃地出門,期權交易也因其危險的投機工具而聲名狼藉。
這也是為什麼你應該只在投機性頭寸上用你能承受損失的錢交易期權。通過將你所有的錢投入到一個單一的未對沖的看漲或看跌期權頭寸來達到槓桿的最大化,以達到定向投機的目的,這是在重複鬱金香狂熱的歷史。
日本90 年代泡沫經濟崩潰
上一個故事裡,我們講述了看漲期權。在這個故事裡,我們繼續介紹另一個重要的期權產品—— 看跌期權。
80 年代以來,日本經濟有兩個極端的表現。 1986 年,日本經濟走勢平穩,由汽車、電子、集成電路等行業帶動,實力逐漸增強,至80 年代末,日本汽車已稱霸全世界,日本的產業在西歐、拉美遍地開花。面對日本經濟繁榮和股市狂漲,日本國民如痴如醉,紛紛投身股市。
1985 年9 月,國際銀行家終於開始出手了。由美英日德法5 國財長在紐約廣場賓館簽署了「廣場協議」,目的是讓美元對其它主要貨幣「有控制」地貶值,日本在美國財長貝克的高壓之下,被迫同意升值。
1987 年10 月,紐約股市崩盤。貝克向日本首相中曾根施加壓力,讓日本繼續下調利率。很快日元利率跌到2.5%,大量廉價資本湧向股市和房地產,東京的股票年成長率高達40% ,房地產甚至超過90%。
此時,東京股票市場已經在3 年之內漲了300%,東京一個地區的房地產總盤子以美元計算,超過了當時美國全國的房地產總值。一個巨大的金融泡沫開始成型。這時候,第一個日經認沽權證在美國證券交易所掛牌,由高盛承銷,發行人為丹麥王國(高盛當時為私人合夥,沒有SEC 註冊資格)。認沽權證(本質與看跌期權相同)給予持有者一定的權利,而非義務,按照事先約定的價格在約定的時間出售標的資產。美國人用大量現金去買,日本人認為根本不可能發生的日本股市暴跌的可能,雙方賭的就是日經指數的走向,如果指數下跌,美國人賺錢,日本人賠錢,如果指數上升,情況正好反過來。
1989 年年底,日本股市達到了歷史巔峰,日經指數衝到了38,915 點,大批的股指沽空期權終於開始發威。高盛公司從日本保險業手中買到的股指期權被轉賣給丹麥王國,丹麥王國將其賣給權證的購買者,並承諾在日經指數走低時支付收益給「日經指數認沽權證」的擁有者。
該權證立刻在美國熱賣,大量美國投資銀行紛紛效仿,日本股市再也吃不住勁了。不可遏制的暴跌就像意外的狂風驟雨劈面向人們襲來,一夜變巨富的美夢化成噩夢深淵,恐慌情緒籠罩著投資者的心。到2003 年4 月最低跌至7,607 點,累計跌幅高達63.24%。
看漲期權和看跌期權
我們首先總結一下看漲期權和看跌期權的概念:
看漲期權是指在協議規定的有效期內,協議持有人按規定的價格和數量購進標的資產的權利。看跌期權是指在協議規定的有效期內,協議持有人按規定的價格和數量賣出標的資產的權利。
看漲期權和看跌期權都屬於衍生品投資範疇內,這意味著他們的價格走勢基於另一種金融資產的價格走勢,這種資產通常被稱為基礎資產。同樣的:
如果交易者預期標的價格在一定時間內上漲,那麼就買入看漲期權。如果交易者預期標的價格在一定時間內下跌,那麼就買入看跌期權。
看漲期權分解
對於美式期權,看漲期權是一項期權合約,使買方有權在到期日之前的任何時間以設定的價格購買標的資產。歐式期權的買方只能在到期日行使期權購買標的。
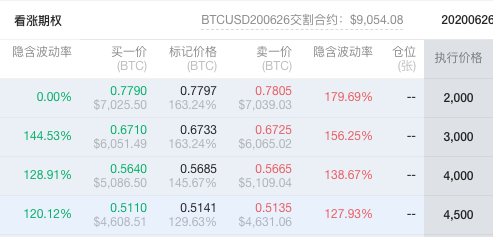
行權價
行權價是看漲期權買方可以購買標的資產的預定價格。例如,OKEx 推出的期權行權價為$2,000 的看漲期權的買方可以在期權到期之前使用該期權以$2,000 的價格購買。
期權到期時間不同,可以是短期的也可以是長期的。只有當標的物的當前價格高於行權價時,看漲期權買方才可以行使期權,並要求看跌期權賣方以行權價賣出,這是值得的。例如,如果比特幣在市場上的交易價格為9,000 美元,則看漲期權買方行使其期權以10,000 美元的價格購買比特幣是不值得的,因為他們可以在市場上以較低的價格購買現貨。
看漲期權買家會得到什麼
以上個例子來說,買權人有權在一定時間內以行使價購買比特幣。為此,看漲期權買方支付權利金。如果標的價格高於行使價,期權將是物有所值的(具有內在價值)。買方可以賣出期權以獲利(大多數人稱其為買方),或者在到期時行使期權(收取比特幣)。
看漲期權賣方會得到什麼
期權買房收取保費。賣出看漲期權是一種產生收入的方式。但是,賣出看漲期權的收入僅限於溢價,而看漲期權買方理論上具有無限的獲利潛力。
計算看漲期權的成本
在OKEx,一張看漲期權合約實際上代表0.1 比特幣。認購價通常以1 比特幣(即10 張期權)報價。
看跌期權分解
對於美式期權,看跌期權是一項期權合同,授予買方權利,在到期日之前的任何時間都可以設定價格出售標的資產。歐式期權的買方只能在到期日行使期權(出售標的)。
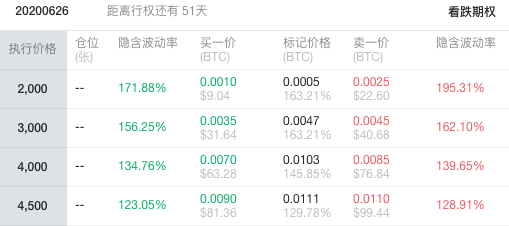
行權價
行權價是看跌期權買方可以以預定價格出售標的資產。例如,行權價為$2,000 的比特幣看跌期權購買者可以使用該期權在期權到期之前以2000 美元的價格出售。
只有當標的物的當前價格低於行權價時,看漲期權買方才可以行使期權,並要求看跌期權賣方以行權價買入標的資產,這是值得的。例如,如果比特幣在現貨市場上的交易價格為9,000 美元,那麼認沽期權購買者便不應該行使其期權以2,000 美元的價格出售,因為他們可以在現貨市場上以更高的價格出售。
看跌期權買方會得到什麼
看跌期權購買者有權在一定時間內以行權價賣出標的資產。為此,看跌期權買方支付溢價。如果標的價格低於行使價,則該期權將是物有所值的。買方可以出售期權以獲利,也可以在到期時行使期權(出售標的資產)。
看跌期權賣方會得到什麼
認沽賣方收取權利金。賣出認沽期權是一種產生收入的方式。但是,賣出看跌期權的收入僅限於溢價,而如果標的資產價格為零,則看跌期權買方的最大獲利潛力就出現了。
計算看跌期權的成本
在OKEx,一張看跌期權合約實際上代表0.1 比特幣,認購價通常以1 比特幣(即10 張期權)報價。
期權的風險參數-希臘字母
「希臘字母」是期權市場中的一個術語,用於描述在特定期權或期權組合中持有期權頭寸所涉及的風險的不同維度。這些變量稱為希臘字母,因為它們通常與希臘符號關聯。每個風險變量都是一個不完全假設的結果,或者是期權與另一個潛在變量之間的關係。交易員使用不同的希臘值(如delta、theta等)來評估期權風險和管理期權投資組合。
隱含波動率
隱含波動率是將市場上的權證交易價格代入權證理論價格模型,反推出來的波動率數值。一個標的波動率代表了該資產的波動劇烈程度及不確定性。與其說隱含波動率決定期權的價格,不如說市場上期權的價格通過波動率反映了市場對該標的波動預期。
δ
δ(Δ) 代表的變化率之間的期權的價格和1 美元標的資產的價格的變化。換句話說,期權相對於標的的價格敏感性。看漲期權的取值範圍是0 到1,而看跌期權的取值範圍是0 到- 1。例如,假設一個投資者做多了一個delta 為0.50 的看漲期權。因此,如果標的股票增加1 美元,期權的價格理論上會增加50 美分。
對於期權交易者來說,delta 也代表了創造delta 中性頭寸的對沖比率。例如,如果你購買0.40 delta 的標準美式看漲期權,你將需要出售40 股股票來進行完全對沖。一個期權投資組合的淨增量也可以用來獲得投資組合的套期保值比率。
θ
θ 代表的變化率之間的期權價格和時間,或時間敏感度——有時被稱為一個期權的時間衰減。表示在其他條件相同的情況下,期權價格隨著到期時間的減少而減少的金額。例如,假設一個投資者做多一個期權,其值為-0.50。在其他條件相同的情況下,期權的價格每天會下降50 美分。如果三個交易日過去,理論上期權價值將下降1.50 美元。
當期權是賺錢的時候,增加,當期權是賺錢的時候,減少。接近到期日的期權也會加速時間衰減。長看漲和長看跌通常都是負的;短線看漲和短線看跌是正的。相比之下,價值不受時間侵蝕的金融工具,如股票,其價值為零。
γ
γ(Γ) 代表Delta 值變化的速度。這被稱為二階(二階導數)價格敏感性。 Gamma 表示在基礎資產中每移動1 美元,delta 的變化量。例如,假設投資者持有假設的XYZ 股票的看漲期權。看漲期權的delta 值是0.50,gamma 值是0.10。因此,如果股票XYZ 增加或減少1 美元,看漲期權的增量將增加或減少0.10 美元。
Gamma 用來確定期權的delta 有多穩定:較高的Gamma 值表明,delta 可能會隨著基礎價格的微小變動而發生劇烈變化。期權正好等於行權價時,伽瑪值較高。伽馬值通常越遠離到期日越小;期限較長的期權對增量變化不那麼敏感。隨著到期時間的臨近,gamma 值通常會變大,因為價格變化對gamma 的影響更大。
期權交易者可能不僅選擇對沖delta,還選擇對沖gamma,以使delta-gamma 保持中性,這意味著隨著基礎價格的變動,delta 將保持接近於零。
Vega
Vega (V) 表示期權價值與標的資產隱含波動率之間的變化率。這就是期權對波動的敏感性。 Vega 表示隱含波動率變化1% 時期權價格的變化量。例如,Vega 值為0.10 的期權表明,如果隱含波動率變化1%,則預期期權價值將變化10 美分。
由於波動性增加意味著標的工具更有可能出現極值,因此波動性的增加將相應地增加期權的價值。相反,波動率的降低會對期權的價值產生負面影響。 Vega 處於平價期權的最高價,這些期權的期限較長,直到到期。
ρ
(p) 表示期權價值與利率變化1% 之間的變化率。這測量了對利率的敏感性。例如,假設看漲期權的rho 值為0.05,價格為1.25 美元。如果利率上升1%,在其他條件相同的情況下,看漲期權的價值將增加到1.30 美元。看跌期權的情況正好相反。 Rho 最適合於到期時間較長的平價期權。
下表簡單總結期權買賣方的Greeks 數值正負關係:
看漲期權看跌期權持有方賣出方持有方賣出方DeltaupdowndownupGammaupdownupdownVegaupdownupdownThetadownupdownup
Conclusion 結語
下期我們將介紹2008 年令大空頭們賺得盆滿缽滿的工具—— 掉期(互換)。














