設G是一個循環群， 
是群中的元素， 
是係數，Multi-Scalar Multiplication (MSM) 是計算多個乘法運算之和
的算法。由於群運算相對於有限域中元素的加法和乘法是複雜的，MSM算法的目標是盡可能減少群運算的次數。通常G是一個定義在有限域
上的橢圓曲線y²=x³+ax+b上的一個循環群，群的階|G|為b ≈ 256比特， 
。如果用樸素的快速冪算法，每個
平均需要1 . 5 b次群運算，總計1 . 5 bn次，下面介紹一些針對較大的n的優化方法。
1 基於窗口方法的優化
我們可以將b 比特的係數拆分成寬度為c 的窗口：將係數寫成
進制
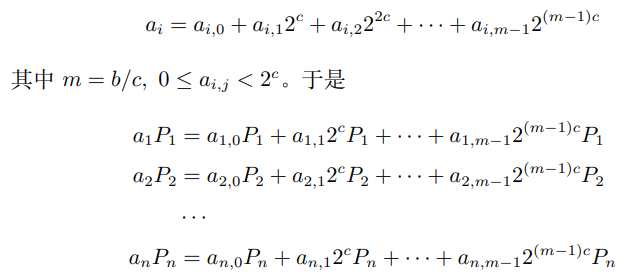
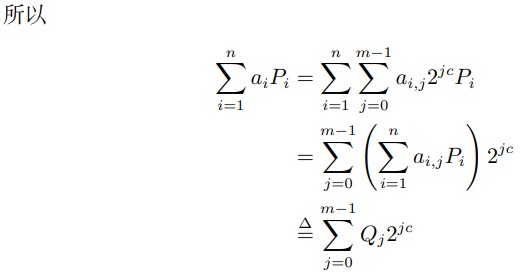
這裡
，於是我們把原先b 比特的MSM 問題轉化為較小的c 比特問題。我們可以提取
中相同的係數(整句翻譯成類似putthe inputs of same scalar into a bucket)，寫為另一種形式：
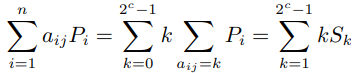
例如當c = 3 時計算
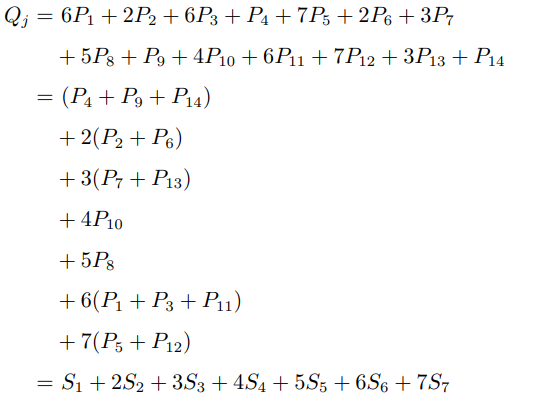
計算
時，令部分和
，於是
而
的計算可以用遞推公式
得到，每個的計算都只需要一次群運算。
在係數大小為c 比特的MSM 時，所有
需要
次群運算，所有
總計需要
次群運算，將這些求和需要
次群運算，所以計算每一個大小為c 的窗口需要
次群運算。計算
只需要用普通的快速冪算法，需要(b/c − 1)(c + 1) = b − c + b/c − 1 次群運算。
綜上所述，寬度為c 的窗口方法一共需要
(1)
次群運算。如果取c = log n，群運算次數就是2bn/ log n，當
時，群運算次數減少為原先的1/12。
2 基於群自同態的優化
對於有限域上的橢圓曲線y² = x³ + ax + b 上的循環群G，如果能找到這樣的群自同態φ：存在
，使得φ(x, y) = (αx, βy) 對G 上的所有點成立。容易證明這樣的自同態是一個乘法映射，即能找到一個λ 使得φ(P) = λP 對所有G 上的點P 成立，這意味著當我們知道了一個點的坐標後，只需對橫縱坐標乘上一個Fp 中的數就能變成另一個點的坐標，這個重要的性質可以對算法進行進一步的優化。
當λ = −1 時α = 1, β = −1 只需要縱坐標取相反數就可以得到一個點的逆。利用這個特性，在樸素的快速冪算法中，可以把係數寫成non-adjacentform (NAF)，即寫成
並且任意相鄰的兩個
不能同時非零。對於b 比特的係數，能讓快速冪算法從原先平均3/2 · b 次群運算降低至4/3 · b 次。這個技巧同樣可以用在窗口方法的優化上。將
寫成
後，執行下面的操作：
可以得到
並且
。由於橢圓曲線群運算中加法和減法複雜度相同，我們可以將這些項按係數的絕對值分組(還是翻譯成bucket)，於是從原先的
組減少為
組，總體所需的群運算次數從(1) 減少為
如果橢圓曲線的參數比較特殊，例如BLS 曲線可以寫成y² = x³+b，並且p ≡ 1 (mod 3)。取
的3 階元素α，存在對應的λ 使得λ(x, y) = (αx, y)
並且λ³ ≡ 1 (mod |G|)。那麼乘法運算可以做如下優化：
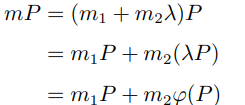
由[1] 我們可以找到足夠小的係數
使得上面的等式成立，這給了我們一個把b 比特的乘法運算轉化為兩個b/2 比特的乘法運算，應用在窗口方法中，群運算的次數減少為
上面兩種優化都可以在
時減少5.5% 的群運算次數。
參考文獻
[1] Francesco Sica, Mathieu Ciet, and Jean-Jacques Quisquater. Analysis of the gallant-lambert-vanstone method based on efficient endomorphisms:Elliptic and hyperelliptic curves. In International Workshop on Selected Areas in Cryptography, pages 21–36. Springer, 2002.
關於我們
Sin7Y成立於2021年，由頂尖的區塊鏈開發者和密碼學工程師組成。我們既是項目孵化器也是區塊鏈技術研究團隊，探索EVM、Layer2、跨鏈、隱私計算、自主支付解決方案等最重要和最前沿的技術。
微信公眾號：Sin7Y
GitHub：Sin7Y
Twitter：@Sin7Y_Labs
Medium：Sin7Y
Mirror：Sin7Y
HackMD：Sin7Y
HackerNoon：Sin7Y
Email：contact@sin7y.org
