統計分析是在一堆獨立的、自身沒有實際意義的數據中尋找可能存在的趨勢、分佈、概率等有意義的信息。統計學的目標是探索和把握數據內在的規律。統計學的應用,簡單來說就是通過蒐集相關數據並進行整理和分析,然後根據數據做出決策。掌握統計學,對日常生活決策也有很大幫助。比如,“十賭九輸”幾乎是人人都知道的基本常識,但所有的賭徒都樂此不疲,原因是都認為自己是那極少數的贏家,都想讓“贏”這一小概率事件發生在自己身上,從而一夜暴富。
統計的基本方法有以下幾點:
1)根據歷史數據,猜測背後的規律
2)基於假設,建立模型,用於描述規律
3)用樣本統計量分佈來估計模型參數
4)用歷史數據來檢驗模型假設
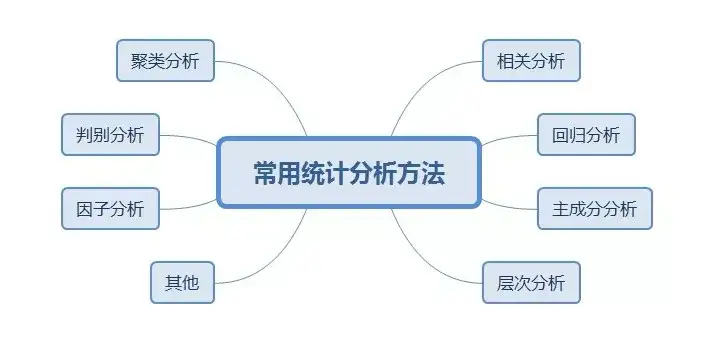
常用的統計分析方法有下面這幾種:
統計在經濟領域的應用非常廣泛,微觀層面,像企業對所售產品的定價決策、市場行情與判斷、市場競爭力都需要進行統計分析;宏觀層面,短期經濟形勢分析和預測判斷通常也都是建立在對經濟統計指標數據分析的基礎之上的。除此之外,國家經濟結構變化、國內外貿易動態、金融證券投資等領域也都離不開統計分析。
隨著金融行業的繁榮與發展,以及金融工具的不斷創新發展,金融市場的複雜程度在不斷加大,統計學在金融領域的應用越來越受到重視。金融是一門立足於經濟現象之上的學科,與統計學之間有著千絲萬縷的聯繫。越來越多的統計方法被用於金融數據分析和金融市場研判。

如上圖所示,統計學的知識體系涵蓋了很多的內容,考慮到本課程的難度和在金融市場中的實用價值,這裡我們主要介紹正態分佈和分位數以及它們在金融領域的應用。
正態分佈
在介紹正態分佈之前,先來看一下什麼是概率分佈。
如果我們想要準確的預測一個變量,我們首先要了解這個變量的基本行為。我們要確定目標變量可能的輸出結果,以及這個輸出結果是離散的還是連續的。以骰子為例,我們首先要知道它可以有的取值範圍,也就是1到6的整數值。下一步就是為事件分配概率。概率越高,事件發生的可能性就越大。當我們大量重複進行實驗得到變量的輸出值,就可以根據這些值作圖,得到的曲線就是概率分佈曲線。目標變量的值的概率就是這一變量的概率分佈。
正態分佈作為一種特殊的概率分佈,不僅曲線優雅,而且在自然界中無處不在,讓你在紛繁的數據背後看到縝密的秩序。
“神說,要有正態分佈,於是就有了正態分佈;神覺得正態分佈不錯,就讓隨機誤差服從了正態分佈。”
正態分佈是一種非常常見的連續概率分佈,常被用在自然科學等領域來表示一個不明的隨機變量:
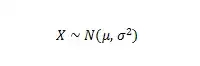
正態分佈的密度函數曲線是中間高兩邊低,由中間向兩邊遞減,並且左右對稱,是一條光滑的“鐘形曲線”:
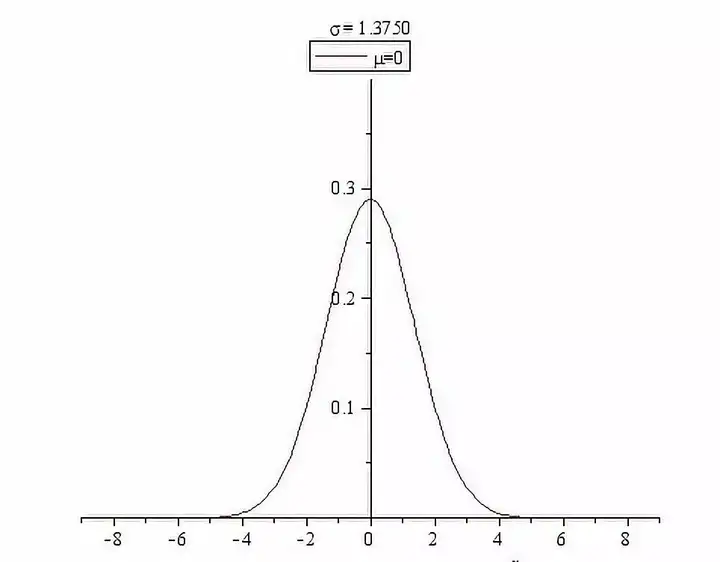
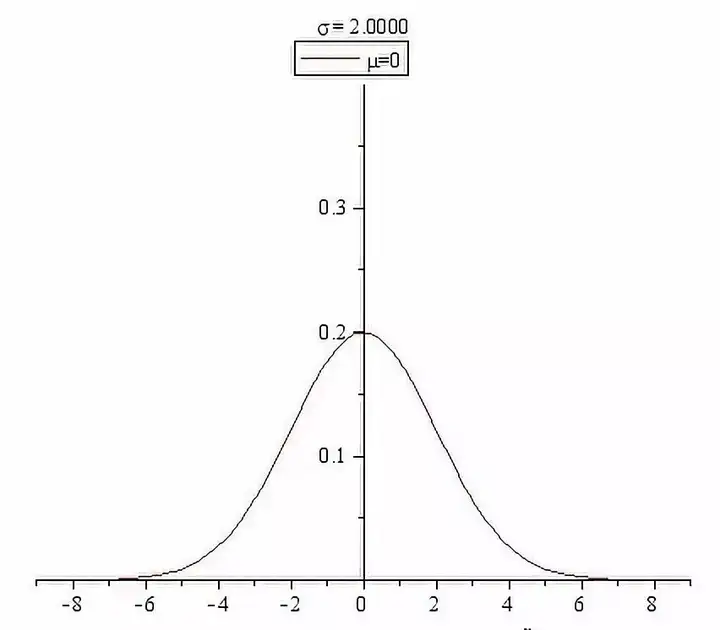
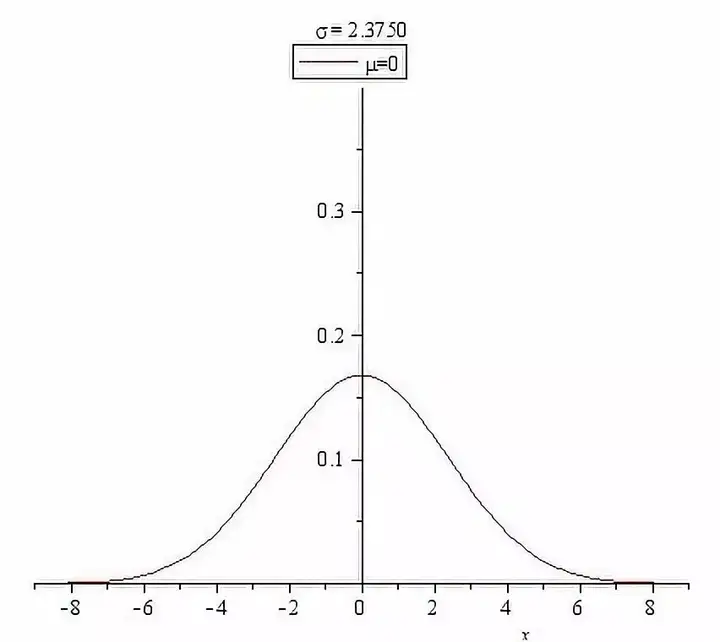
正態分佈距離均值越近的地方數值越集中,距離均值越遠的地方數值越稀疏;這意味著正態分佈出現極端值的概率很低,而出現均值附近的數值的概率非常大。
正態分佈的密度函數如下:
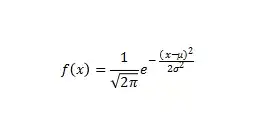
其標準化後的概率密度函數為:
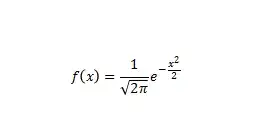
正態分佈有以下特性:
集中性:正態曲線的高峰位於正中央,即均數所在的位置;
對稱性:正態曲線以均數為中心,左右對稱,曲線兩端永遠不與橫軸相交;
均勻變動性:正態曲線由均數所在處開始,分別向左右兩側逐漸均勻下降。
正態分佈又被稱為高斯分佈。德國的10馬克紙幣上有高斯的頭像和正態密度曲線:

正態分佈在統計中是非常常用的分佈,例如在醫學上,可以應用正態分佈估計人體的某些生理指標,比如白細胞數的正常值範圍,白細胞數在正常人群中近似服從正態分佈。此外,各種各樣的心理學測試分數和物理現像比如光子計數都被發現近似地服從正態分佈。
在金融數據的分析中,很多情況下我們會假設數據滿足正態分佈,例如證券的收益率和價差等。在一些量化交易策略中,正態分佈也為我們提供了許多便捷,例如很多配對交易策略,就是以證券對之間的價差變化服從正態分佈為假設前提的。
借助萬礦量化平台,利用正態分佈假設,我們可以實現一個較為簡單的期貨套利策略:
首先假設期貨的價差服從正態分佈,可以利用其漲跌幅的相關性進行套利。由於螺紋鋼和熱軋捲板的走勢存在較強的相關性,我們使用螺紋鋼和熱軋捲板的數據,繪製其收盤價差以及上下軌:
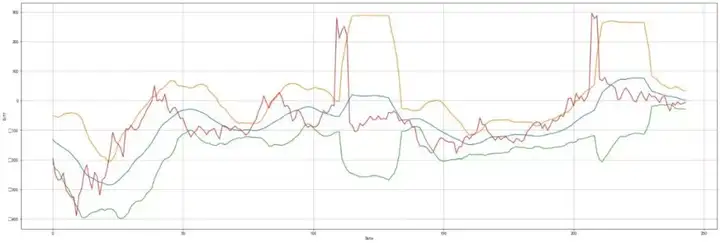
這部分的代碼如下:

我們簡單的在價差上穿上軌線時做多螺紋,做空熱捲;在價差下穿下軌線時做空螺紋,做多熱捲,價格觸及均線時,清空倉位。這個策略的回測結果如下:
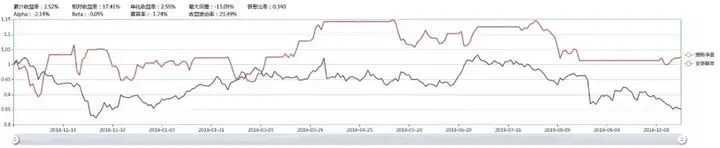
可以看到,這個策略的年化收益率為2.59%。
有關交易策略和量化實現的內容我們在ALPHA Library的高級課程中會具體講解,這裡僅作為了解。
分位數
分位數的英文名稱是Quantile,是指將一組數據劃分為成一定比例的數值點,常用的有中位數、四分位數、百分位數等。把一組數據進行排序,然後取25%位置、50%位置、75%位置或是其他位置的數據,就成為分位數。
眾數、中位數、分位數、均值、幾何平均數、切尾均值都是表徵集中趨勢的指標。當數據分佈在偏度上偏離正態分佈時,算術平均數、中位數、眾數之間有這樣的特徵:右偏時:算術平均數>中位數>眾數;左偏時:眾數>中位數>算術平均數。正態分佈情況下眾數、中位數、算術平均數相等。
分位數存在的意義在於,當數據存在偏態的時候,只看數據的中間位置略有不妥,希望同時保有中位數穩健的特性,又要對“中間”進行修正,可以使用25%或是75%分位數,通過這兩個分位點的數據來判斷總體水平。
分位數在生活中有很多應用場景。例如在考試的排名中, 如果75%分位數是80分,這就意味著80分以上的同學能夠排進前25%。再比如在討論一個城市的平均工資時,高收入的人群其收入遠大於低收入的人群,就會出現“被平均”的現象,於是使用分位數是比較好的選擇,使用分位數可以清晰的看到你的工資水平處於前百分之幾,也就是比這個城市中多少人高,而不是簡單的和“被平均”的平均工資比較。
在金融研究領域,分位數回歸在股票、期貨的風險測量和演化模式分析、IPO定價行為、基金流量決定因素分析、CAPM模型、高頻金融數據價量關係、資本結構選擇等方面頻繁使用。
在金融市場中,分位數也是一個簡單而實用的工具。如果要衡量市場上全部基金的表現進而挑選合適的基金時,可以使用分位數,比如90%分位數,這樣挑選出來的基金就是在業績上打敗了90%的其他基金。在進行指數基金定投時,如果指數PB低於歷史某個分位數的時候,可以加大定投的力度。
統計學其他理論方法在金融中的應用
通過協整檢驗、ECM模型、非平穩時間計量經濟模型、VaR模型等的運用,統計學對我國貨幣政策效率、貨幣供給對產出和價格的影響、人民幣匯率波動造成的物價水平波動、相關財政政策和貨幣政策刺激經濟增長原理分析等宏觀數據的實證研究做出了不小的貢獻。
用統計方法研究金融市場比較典型的是VaR的運用和具有異方差的時間序列模型技術的應用。近年來,神經網絡等機器學習在金融市場中的應用也越來越多。
統計學的理論方法不是最重要的,我們需要養成提出假設、將實際應用問題抽象為數學問題、並能進行分析驗證的統計思維。















