PART4.Modelling

平穩性檢驗-如果一個時間序列(或隨機過程)的聯合概率分佈在時間或空間平移下不變,則它被定義為強平穩。特別重要的是,對交易員來說,這個過程的均值和方差不會隨時間或空間而變化,而且它們都不會跟隨趨勢。
平穩價格序列的一個重要特徵是,序列內的價格從初始值擴散的速度比GBM慢。通過測量這種擴散行為的速率,我們可以確定時間序列的性質,從而檢測它是否是均值回歸。現在我們將概述一個算法,即赫斯特指數,它幫助我們描述時間序列的平穩性。
赫斯特指數-Hurst指數的目標是為我們提供一個標量值,它將幫助我們識別(在統計估計的範圍內)一個序列是均值回歸、隨機遊走還是趨勢。
赫斯特指數計算背後的思想是,我們可以使用對數價格序列的方差來評估擴散行為的速率。任意時間滯後τ,τ的方差是由:
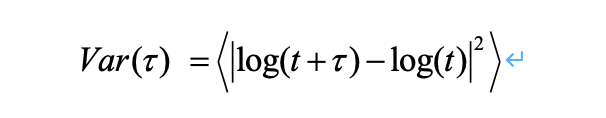
大括號中的內容指的是所有t的均值。
其目的是將擴散速率與GBM進行比較。在GBM的情況下,在大的時間(即τ較大時)τ的方差與τ成正比:

如果我們發現與這種關係不同的行為,那麼我們就確定了是趨勢或均值回歸序列。關鍵的觀點是,如果任何連續的價格走勢具有非零相關性(稱為自相關性),那麼上述關係是無效的。相反,可以將其修改為包含一個指數值“2H”,得到Hurst指數值H:
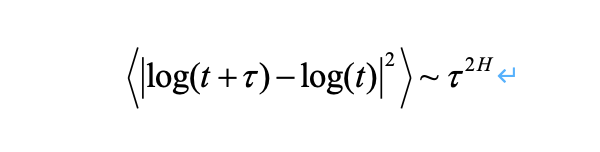
因此,可以看出,如果H = 0.5,我們有一個GBM,因為它只是變成了之前的關係。然而,如果h

0.5,則有趨勢或均值恢復行為。特別是:
● H < 0.5 -時間序列為均值回复
● H = 0.5 -時間序列是一個幾何布朗運動
● H > 0.5 -時間序列是趨勢
除了描述時間序列的特徵外,赫斯特指數還描述了範圍。以分類的方式表現的系列。例如,接近0的H值是一個高度平均的恢復序列,而接近1的H值則是一個強烈的趨勢。
要計算Amazon price系列的Hurst指數,如上文解釋ADF時所使用的,我們可以使用以下Python代碼:
from __future__ import print_function from numpy import cumsum , log , polyfit , sqrt , std , subtract from numpy.random import randn def hurst ( ts ): """返回时间序列向量t的Hurst指数""" # 创建滞后值的范围lags = range ( 2 , 100 ) # 计算滞后差的方差数组s tau = [ sqrt ( std ( subtract ( ts [ lag :], ts [: - lag ]))) for lag in lags ] # 使用线性拟合估计赫斯特指数poly = polyfit ( log ( lags ), log ( tau ), 1 ) # 从polyfit输出返回Hurst指数return poly [ 0 ] * 2.0 # 创建一个Gometric brown Motion, Mean-Reverting and trends序列gbm = log ( cumsum ( randn ( 100000 )) + 1000 ) mr = log ( randn ( 100000 ) + 1000 ) tr = log ( cumsum ( randn ( 100000 ) + 1 ) + 1000 ) # 输出上述每个序列的Hurst指数# 以及亚马逊的价格(调整后的收盘价) # 本文给出的ADF测试print ( "Hurst(GBM): %s " % hurst ( gbm )) print ( "Hurst(MR): %s " % hurst ( mr )) print ( "Hurst(TR): %s " % hurst ( tr )) # 假设您已经运行了上面的代码来获得' amzn ' ! print ( "Hurst(AMZN): %s " % hurst ( amzn [ ' Adj Close ' ])) Hurst指數的Python代碼輸出在下方給出:
Hurst(GBM): 0.502051910931 Hurst(MR): 0.000166110248967 Hurst(TR): 0.957701001252 Hurst(AMZN): 0.454337476553 從這個輸出我們可以看到,GBM的赫斯特指數H幾乎正好是0.5。回歸序列的平均H幾乎等於零,而趨勢序列的H接近於1。
有趣的是,Amazon的H也接近0.5,這表明它類似於GBM,至少在我們使用的樣本期間是這樣!
更多內容請關注公眾號【火象】~














