原標題:《UniV3的數學原理》
作者:比原鏈研究院
前言——Uniswap V3(如下簡稱Uni V3)放出了很多feature,然而其最為本質的迭代依然是對AMM 數學曲線的再思考。在過去的兩年中,我們也躬身入局AMM 領域,認為AMM 最基本的曲線形態已經定型,後續的創新應該會在AMM 基本曲線形態的基礎上實現“策略化”,於是我們創造了MOV 超導V2。而如今我們看到了V3,突然有一種“久別重逢”的感覺,在尋找這種感覺之餘,我們也希望為大家呈現AMM 最為深刻的思考路程。因為AMM 的時代將會比想像得更為恢弘壯闊。
讓我們直切正題,Uniswap V3 最耀眼的創新——在AMM 上實現集中流動性。
V3 給出了一個虛擬儲備金(virtual reserves)的概念,舉例講解:
在傳統V2 中,Alice 一次性將500,000 DAI 和333.33 ETH 注入儲備池,總價值$1m,提供全區間(0,infty)的流動性,但實際上ETH 的價格波動範圍在很長一段時間內是有局部範圍的,這種為全區間無私提供流動性的行為大大浪費了資本利用效率。
(注:在一個逐步走向成熟化的金融市場中,無套利原理和提升資本利用效率永遠是兩大核心訴求,也是後續DeFi 產品向先驅DeFi 發起挑戰的出發點。)
所謂的集中流動性便是讓LP 自主選擇波動範圍,只為該範圍提供局部流動性,例如Bob 認為未來一段時間內ETH 的價格區間在(1000,2250),並且如果未來真的是在這個區間波動,Bob 希望自己獲得的收益能夠跟百萬富豪Alice 一樣多,於是Bob 一開始只需要投入91,751 DAI 和61.17 ETH,總價值$183,500,遠遠小於Alice 實際投入的資金。我們對照下圖來解釋其中的道理。
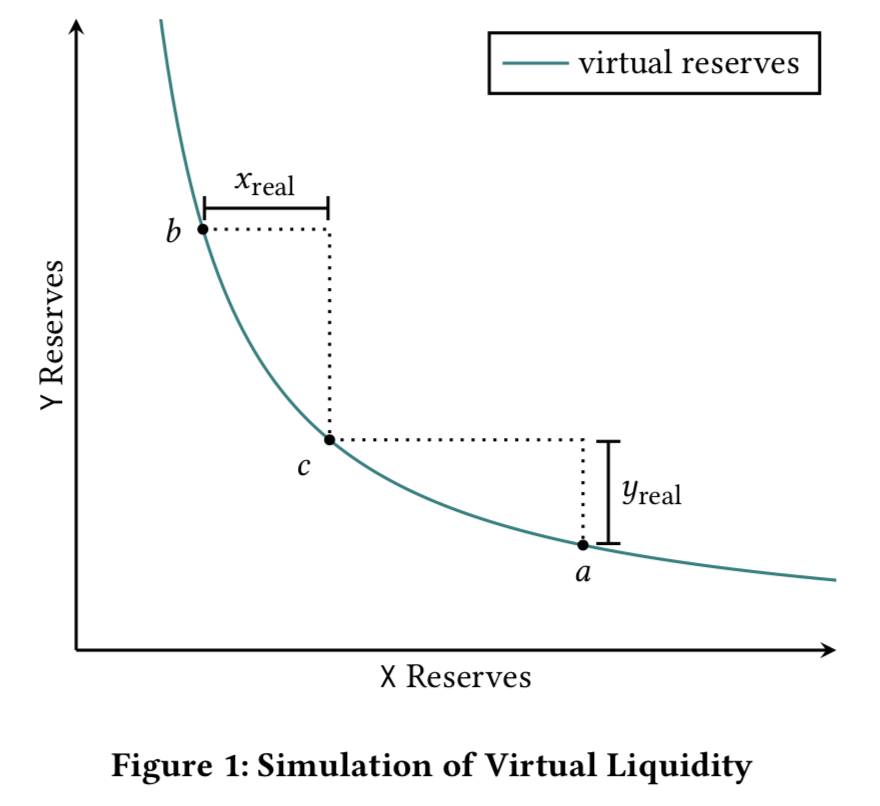
其中,X 是ETH,Y 是DAI,點a 對應價格1000,點b 對應價格2250,點c 是當前市場價格1500,x_{real}是Bob 投入的61.17 ETH,y_{real}是91751 DAI。
在數學實現上——假設圖中曲線表達式為xy=D,其中D 便是我們要確定的值,即這條“虛擬的”曲線。
存在如下客觀事實:
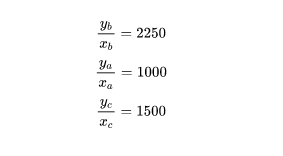

進一步,由於

則

解方程得

最後我們發現
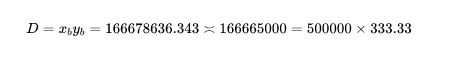
即Bob 所獲得的虛擬曲線(D 值)幾乎跟Alice 一樣。
上述計算過程是一種反證法,實際上用戶Bob 會向系統算法提出自己的需求輸入,包括預測價格區間範圍、當前價格點、最終想要獲得的一個virtual reserves 規模(即虛擬曲線D 值)。有了虛擬曲線表達式的確定,可以輕鬆算出a、b、c 三個確定的點坐標,進而便算出 x_{real}=61.17 以及y_{real}=91751。
同時,也可以看到,一旦未來價格越出了區間,Bob 其中一種資產將徹底消失。

虛擬儲備金(virtual reserve)是Uni V3 實現集中流動性的基礎原理,也是Uni V3 將多樣化的倉位區間統一成一條(大的全區間的虛擬)曲線的巧妙之處。然而看似簡單的原理背後缺需要復雜的工程實現和算法模型的支撐,尤其是解決手續費(fee)的統計計算和LP 的加入/退出計算。
對於AMM 來說,最複雜的莫過於LP 的存取行為和收益統計,在以V2 為代表的經典AMM 模型中,會通過一種“份額模式”從始至終為LP 確定下各自可提取的數量比例(也包括手續費)。但在V3 中,將會對LP 可提取比例以及所獲fee 比例進行一種“非常統計風格”的計算方法。
在具體實現上,Uni V3 將價格全區間以ticks 的模式均勻分段,變成離散的空間:

如何根據當前價格,判斷所處ticks——
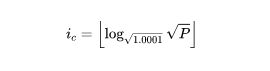
全局狀態中有feeGrowthGlobal0(f_{g},0) 和feeGrowthGlobal1 (f_{g},1)—f_{g},用來從全局角度統計總的手續費收益。例如,當在一個tick 內發生了一筆交易,系統會計算出該筆交易產生的手續費:

其中y_{in}為該筆交易的輸入數量,其餘部分是手續費的比例。系統會不斷累計出每個tick 內產生的所有手續費總和。
再引入一個“稍微低一個級別的”全局狀態變量feeGrowthOutside{0,1}—f_{o},用於計算在給定區間(range,由很多連續的ticks 組成的空間)內的手續費總和。我們想查詢某個價格range(即在下界tick i_{l}和上界tick i_{u}之間)產生了多少累計手續費,總公式為:
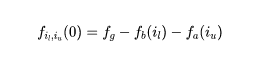
其中,

f_{a}變量是對所有高於i tick 的區間的fee 統計,f_{b}是對所有低於i tick 的區間的fee 統計,因此在上述總公式中,我們從全局總累計手續費f_ {g}中減去所有低於下界i_{l}的累計手續費,再減去所有高於上界i_{u}的累計手續費,便是(i_{l},i_{u}) 之間的累計手續費。
f_{o} 可以理解為一個計算單元,用於累積截止到i tick 的手續費,在它的初始化過程中,我們約定如下:
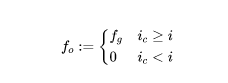
再來看f_{a}的計算,分成了兩段,可以理解為——
如果當前tick 等於i 或者高於i,此時從全局總手續費f_{g} 中減去“累積到i tick”的手續費f_{o}(i),剩下的便是對所有高於i tick 的區間的fee 統計;但如果當前tick 還未抵達i,此時根據對f_{o} 的初始化定義為0,則所有高於i tick 的區間的fee 統計尚未產生,為0。
同樣對於f_{b}——
如果當前tick 抵達或者超過了i,f_{o}(i)表示累計到i 的手續費,也即對所有低於i tick 的區間的fee 統計;如果當前tick 還未抵達i,對所有低於i tick 的區間的fee 統計值即為當前的全局變量f_{g}(當前總手續費)。
通俗來概括,系統算法要統計某一個range 內累計的手續費,
如果當前tick 已經處於range 內部,即i_{l}leq i_{c} < i_{u},只需要從全局手續費f_{g}減去所有低於i_{l}組成的range 累計的手續費;如果當前tick 不處於range 內部,且低於下界i_{l},說明尚未在(i_{l},i_{u})區間內產生交易,也就未產生手續費,因此該range 內累計量為0;如果當前tick 不處於range 內部,且高於上界i_{u},需要從全局總量中分別去除“兩頭”各自的累計量,即從全局f_{g}中減去所有低於i_{l}區間累計量,再減去“從i_{u}到當前tick 區間累計量”。
Uni V3 計算手續費的過程是一種從微觀走向宏觀的思想,它將空間劃分成離散的,每一個時間刻度只會在一個離散空間上產生交易,從而產生手續費,每一個微觀tick 都在各自記錄著自己從最低tick 到自身這段區間內的累計手續費總和,然後供上述公式不斷調用,以計算各種宏觀結果。
Uni V3 已經改變了傳統AMM 對LP 行為的設定,也不再基於全局流動性(Global Liquidity)和份額(Share)來為每一個LP 計算手續費收益。對V3 來講,它只關注在每一個tick 裡存在多少“虛擬”流動性,以及這些虛擬流動性產生了多少手續費,算得單位虛擬流動性對應的手續費值;在這個時空之下,我們再把視角切到具體每一個LP 上,對於任何LP,都會存在一個“開倉”(Position)的區間設定,他在自己設定的區間提供了虛擬流動性,可能是一個tick,也可能是連續多個tick,從最簡單的“一個tick”角度解釋,系統會記得同一時空下每一個LP 在此tick 注入的虛擬流動性值,並為他們確定出一個比例(注意這個比例只與最開始注入的虛擬流動性大小有關,並不涉及手續費轉流動性,這與V2 是不同的),以此分得該tick 內所有手續費累計。

在實際情況中, LP 們還會存在復雜的行為,比如注入/退出的時間紛雜、選擇的range/tick 紛雜。但Uni V3 的大道至簡之處正是利用全局計算來屏蔽掉單個LP 視角,只關心ticks 視角和Position 視角。在確定好上述所述的一系列全局狀態變量的定義後,認真記錄好每一筆swap 交易在ticks 中發生的情況(包括只在一個tick 內完成該筆swap 交易,和需要跨多個tick 才能完成該筆swap 交易),同時只記錄每個tick 內虛擬流動性的大小,以此為根本去提供swap 交易公式以及swap 後手續費如何分配給參與該tick 的所有LP 們。 LP 的複雜行為體現在空間的不連續性和時間的不統一性兩方面,對於時間不統一性(即會出現很多LP 不斷加入和退出流動性),Uni V3 還會引入Position 這一級別的全局變量為每一個身份(address)記錄下其對range/tick 加入/退出(“setPosition”)時手續費的統計(uncollected fee/feeGrowthInside),確保後來的LP 不會參與到前序LP 們已經累計的收益分配。
如果總結來講,tick-level 是對空間上發生的統計,確保起點一致的LP 們fee 分配,而Position-level 是對時間上發生的統計,確保不同起點的LP 們fee 累計起點不一樣。建議實現者深入V3 代碼,才能真正獲得安全計算法。
最後,Uni V3 過於復雜,但大道至簡,即便去模仿,模仿者依然需要下功夫深刻了解其“微積分”思維。這篇文章只選擇了fee 這一個角度呈現Uni V3 的“數學原理”,也是其實現集中流動性的核心邏輯。而在數學之外,我們有更多驚喜的“哲學意義”發現與大家分享,例如LP token 的進化、NFT 其實並不只屬於藝術領域(更有助於金融)、V3 會存在一個策略博弈、V3對基金池/合成資產的啟示等等,當然也包括與MOV 超導V2 的“心有靈犀”——AMM 的本質是連續性的無限網格,Uni V3 是在這個無限網格基礎之上再實現了微觀無限網格,是“無數網格機器人的疊加”,MOV 超導V2 則是在無限網格基礎之上進行了更為宏觀的無限網格,是超級網格。請期待下一篇《Uni V3 的自然哲學》。
















