成功的量化交易PART 5-績效和風險管理(8)

火象趣交易｜2021-11-03 11:21

PART5.Performance and Risk Management

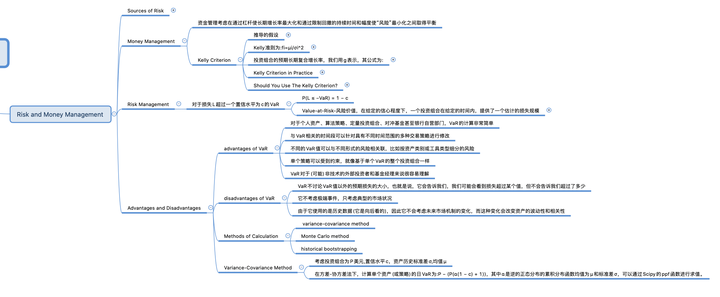
優勢和缺陷

VaR在金融行業中非常普遍，因此您應該熟悉這種技術的優點和缺點。 VaR的一些優勢如下:

● 對於個人資產、算法策略、定量投資組合、對沖基金甚至銀行自營部門，VaR的計算非常簡單。

● 與VaR相關的時間段可以針對具有不同時間範圍的多種交易策略進行修改

● 不同的VaR值可以與不同形式的風險相關聯，比如按資產類別或工具類型細分的風險。例如，這使得我們很容易解釋投資組合風險集中在哪裡。

● 單個策略可以受到約束，就像基於單個VaR的整個投資組合一樣。

● VaR對於(可能)非技術的外部投資者和基金經理來說很容易理解。

然而，VaR也並非沒有缺點:

● VaR不討論VaR值以外的預期損失的大小，也就是說，它會告訴我們，我們可能會看到損失超過某個值，但不會告訴我們超過了多少。

● 它不考慮極端事件，只考慮典型的市場狀況。

● 由於它使用的是歷史數據(它是向後看的)，因此它不會考慮未來市場機制的變化，而這種變化會改變資產的波動性和相關性。

VaR不應該單獨使用。它應該始終與一套風險管理技術一起使用，例如多樣化、最佳投資組合配置和謹慎使用槓桿。

計算方法-到目前為止，我們還沒有討論實際計算的VaR，無論是在一般情況下或一個具體的交易例子。我們會對三種技術感興趣。第一種是方差-協方差法(使用正態性假設)，第二種是蒙特卡羅方法(基於潛在的非正態分佈)，第三種是歷史自舉法，它利用歷史收益信息來評估資產。

在這一節中，我們將集中討論方差-協方差法。

方差-協方差法-考慮一個投資組合為P美元,置信水平c。我們正在考慮日常的回報,與資產(或策略)歷史標準差σ,均值為µ。然後，在方差-協方差法下，計算單個資產(或策略)的日VaR為:

P − (P(α(1 − c) + 1))

其中α是逆的正態分佈的累積分佈函數均值為µ和標準差σ。

我們可以使用SciPy和pandas庫來計算這些值。如果我們設置P = 106和c = 0.99,我們可以使用SciPy的ppf方法生成逆累積分佈函數值，且服從均值為µ方差為σ的正態分佈，從而獲得一些在這種情況下,花旗集團的歷史每日回報的真正的財務數據(我們很容易代入算法策略的回報):

 #!/usr/bin/python # -*- coding: utf-8 -*- # var.py from __future__ import print_function import datetime import numpy as np import pandas.io.data as web from scipy.stats import norm def var_cov_var ( P , c , mu , sigma ): """方差-每日风险值的协方差计算使用置信水平c，均值为mu投资组合的标准差sigma价值P """ alpha = norm . ppf ( 1 - c , mu , sigma ) return P - P * ( alpha * （ 1 - c ） + 1 ) if __name__ == "__main__" : start = datetime . datetime ( 2010 , 1 , 1 ) end = datetime . datetime ( 2014 , 1 , 1 ) citi = web . DataReader ( "C" , ' yahoo ' , start , end ) citi [ "rets" ] = citi [ "Adj Close" ] . pct_change () P = 1e6 # 1,000,000美元c = 0.99 # 99%置信区间mu = np . mean ( citi [ "rets" ]) sigma = np . std ( citi [ "rets" ]) var = var_cov_var ( P , c , mu , sigma ) print ( "Value-at-Risk: $ %0.2f " % var )