STARKs 是一類交互式證明系統,但為了本教程的教學目的,最好將其視為SNARKs 的一個特例,其中:
哈希函數是唯一的密碼學成分;
算術化基於代數中間表達(AIR - algebraic intermediate representation ),並將關於計算完整性的要求化簡為關於某些多項式的低度(low-degree)的要求;
多項式的低度是通過使用FRI子協議來證明的,而FRI 本身是通過默克爾樹來實現的(作者註:FRI 被定義為可在任意位置進行查詢的抽象預言機。因此,FRI 協議可以通過模擬使用密碼學向量承諾方法的預言機而被編譯成具體協議。Merkle 樹提供了此功能,但並不是唯一能做到這一點的密碼學原語。);
零知識是可選項。
本教程的這一部分是解釋STARKs 的定義中的一些關鍵術語。
在計算複雜性理論中,交互式證明系統是一個至少基於兩方的協議,其中一方(即驗證者)只有在某一數學聲明為真時才會確信其正確性。在理論上,這個聲明可以是任何可以用數學符號表達的東西,比如“貝赫和斯維納通-戴爾猜想”、“P≠NP 問題” 或'第十五個斐波那契數是643617 '。 (在一個可靠的證明系統中,驗證者會拒絕最後一個聲明)
密碼學證明系統將“交互式證明系統”的這一抽象概念轉化為可以在現實世界中應用部署的具體對象。而在現實世界進行應用的限制也帶來了一些相應的簡化:
這個聲明不是關於一個數學猜想,而是關於一個特定計算的完整性,比如'電路C 在輸入x 後得到輸出y',或'圖靈機M 在T 步之後得到輸出y'。這種證明系統被稱為建立了“計算完整性”。
該協議有兩方,證明者和驗證者。在不失一般性的情況下,驗證者發給證明者的消息由純粹的隨機參數組成,在這種情況下(幾乎總是這種情況),證明系統可以通過Fiat-Shamir 變換轉變為非交互式證明系統。非交互式證明系統只包括從證明者到驗證者的單一信息。
與其說是實現了絕對安全,不如說驗證者可以接受一個非零但小到可以忽略的“假陽性”或“假陰性”的可能。或者說,在證明者擁有有限計算能力的前提下,該證明系統可以提供真正的安全性。畢竟,所有真實計算機的計算能力都是有上限的。有時作者們會使用術語“論證系統”來區別於“證明系統”,後者提供了針對擁有無限計算能力的證明者的安全性;使用“論證”指代由非交互性變換產生的“對話腳本“。
為什麼驗證者不能簡單地重新運行計算完整性聲明所包含的計算呢?這是因為證明者擁有驗證者無法獲得的資源。
當受限制的資源是時間時,驗證者的運行速度應該比程序的簡單重新執行快一個數量級。實現這一特性的證明系統被稱為簡潔的( succinct )或具有簡潔的驗證過程。
簡明驗證過程需要簡短的證明,但一些證明系統,如Bulletproofs 或Aurora,具有緊湊簡潔(compact)的證明,但驗證者的驗證過程仍十分緩慢。
當驗證者不能接觸到證明者使用的秘密信息,而證明系統又能保護這一秘密的隱私性時,證明系統就滿足了零知識性。驗證者可以確信一個計算聲明的真實性,同時不知道關於該計算的某些或全部的輸入信息。
特別是在零知識證明系統的背景下,計算的完整性要求可能需要一個微小的修正。在某些情況下,僅僅證明一個聲明的正確性是不夠的,證明者還必須另加證明:他知道額外的秘密輸入,而且還可以直接輸出秘密而不僅僅是產生證明(作者註:正式來說,“知識”的定義如下:必須存在一種“提取器”算法,該算法具有對“可能是惡意的證明者”的預言訪問權,假裝是匹配的驗證者(能讀取來自證明者的消息並通過相同的接口發送自己的消息),有能力通過“倒帶”的方式,將“可能是惡意的證明者”倒退到任何較早的時間點,整個過程以多項式時間運行,並輸出證據witness 。STARKs 已被證明滿足這一特性,見EthSTARK 文檔的第5 節)。能實現這種具有知識健全性概念的證明系統被稱為知識證明(或知識論證)。
SNARK 是一個簡潔的非交互式知識論證( Succinct Non-interactive ARgument of Knowledge ) 。創造了SNARK 這個術語的論文用簡潔( succinct )來表示具有高效驗證者的證明系統。然而,近年來,這個術語的含義已經被淡化,現在這個術語包括任何證明是緊湊( compact )的系統。本教程內容皆基於原始論文定義。
STARK 是“可擴展透明知識論證”( Scalable Transparent ARgument of Knowledge ) 的縮寫。可擴展(Scalable)指的是兩件同時發生的事情: (1) 證明者的運行時間最多只能與計算的規模成擬線性關係,這與SNARKs 不同。在SNARKs 中,證明者被允許擁有一個高到令人望而卻步的時間複雜性;(2) 驗證時間與計算的規模成多項式對數關係。透明(Transparent)是指所有驗證者的信息只是公開採樣的隨機值。特別是,不需要可信的設置儀式來實例化證明系統,因此不存在密碼學上的'有毒廢物'。這個縮寫的含義表明,非交互式STARKs 是SNARKs 的一個子類,事實上也是如此,但是這個術語一般用來指可擴展的透明SNARKs 的具體構造。
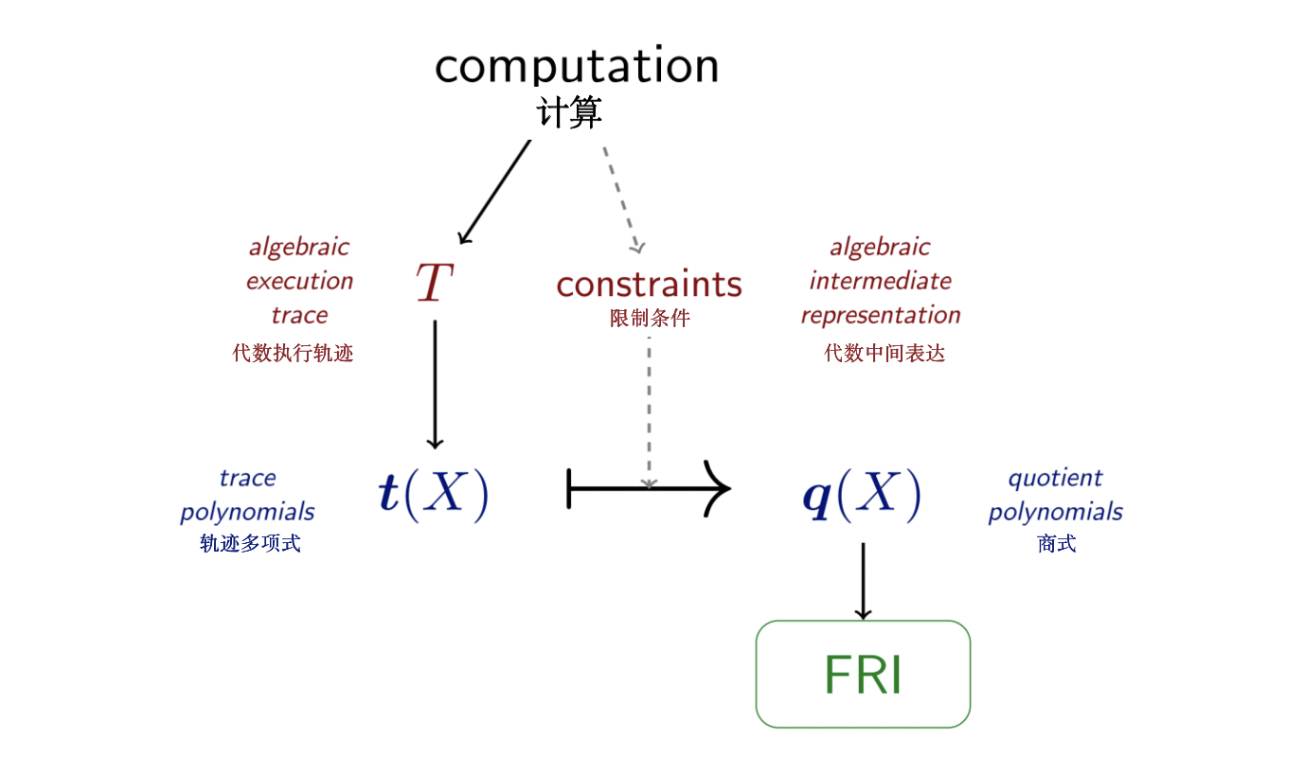
用編譯流水線的方法可以最直觀的展示STARK的主要特性。根據細化程度的不同,我們可以選擇將這個過程細分為更多或更少的步驟。在這裡,為了介紹STARKs ,編譯流程被分為四個階段和三次轉換。在本教程的後續部分,會有一個更精細的編譯流程和圖表。
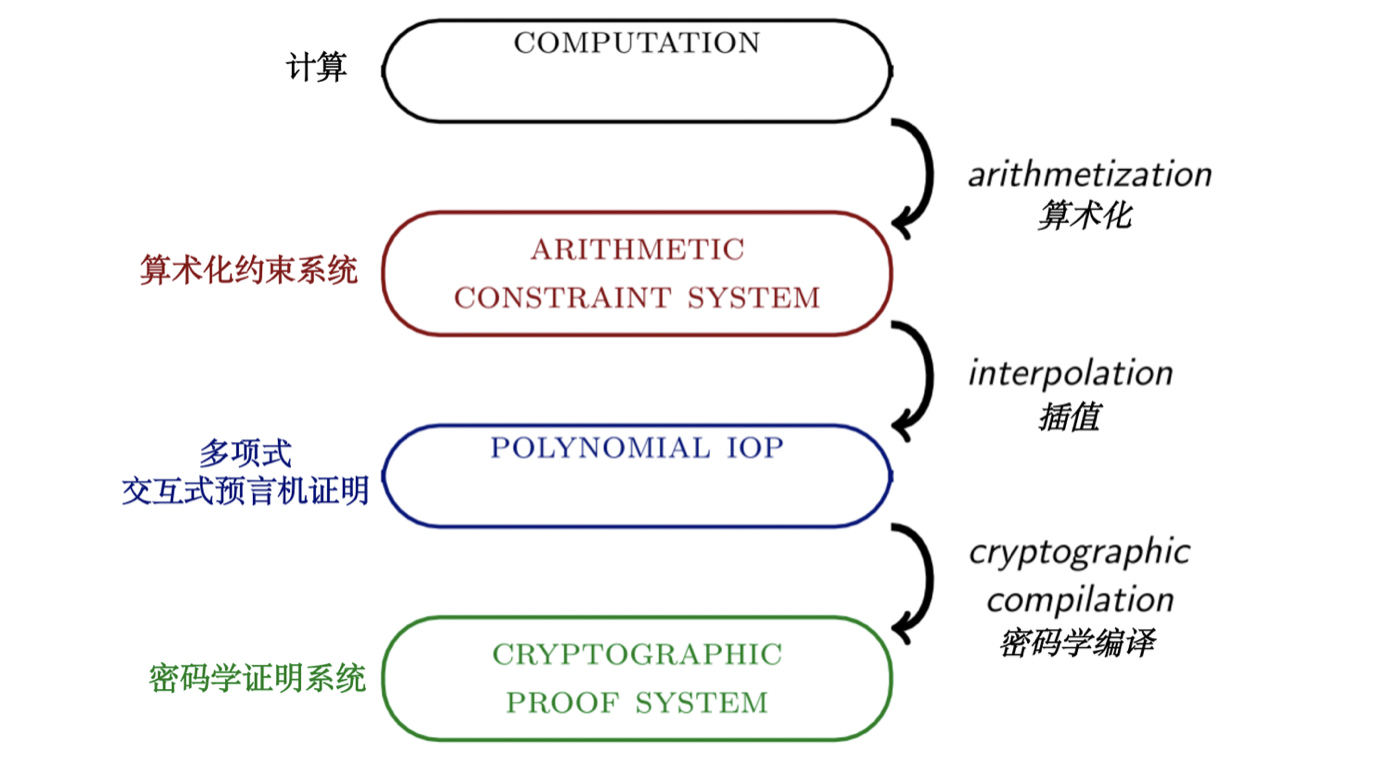
整個流程的輸入是一個計算過程,你可以把它看成是一個程序、一個輸入和一個輸出。這三者都是以機器友好的格式提供的,比如一個字節的列表。一般來說,程序由指令組成,這些指令決定機器如何操作其資源。如果一個機器的某種正確的指令集可以模擬任何圖靈機,那麼可以說這個機器的架構是圖靈完備的。
在本教程中,程序被硬編碼到機器架構中。因此,允許用於計算的空間是相當有限的。儘管如此,輸入和輸出仍然是可變的。
一個計算所需要的資源可能是時間、內存、隨機性、秘密信息、並行性。我們的目標是將計算過程轉化為另一種形式,使得即使是資源受限的驗證者也能夠輕鬆驗證其完整性。除上述計算資源之外,還有更多類型的資源可供研究探討,比如糾纏的量子比特、非確定性、或者計算一個給定的黑盒函數的預言機,但由此產生的問題通常是計算複雜性理論的主題,而不是密碼學實踐應該探討的話題。
流程中的第一個轉換被稱為算術化(arithmetization) 。在這個過程中,用比特流表示的基本的邏輯和算術運算序列被轉化為有限域元素的運算操作序列,從而使兩者代表相同的計算過程。計算輸出是一個算術化約束系統,本質上是一串方程,所有方程的係數和變量的取值都來自有限域。當且僅當算數化約束系統有一個令人滿意的解決方案(有正確解)時,計算才是完整的——也就是說,存在對變量的單一賦值使得所有方程都成立。
STARK 證明系統對計算的算術化過程如下。在任一時間點上,計算的狀態都包含在一個元組中(一個元組包含w 個寄存器),這些寄存器從有限域 中取值。機器內定義了一個狀態轉換函數
中取值。機器內定義了一個狀態轉換函數 ,每個週期都會更新寄存器狀態。代數執行軌跡(AET)是按時間順序排列的所有狀態元組的列表。
,每個週期都會更新寄存器狀態。代數執行軌跡(AET)是按時間順序排列的所有狀態元組的列表。
算術化約束系統在代數執行軌跡上至少定義了兩類約束:
邊界約束:在計算階段的開始或結束時,一個指定的寄存器有一個給定的值。
狀態轉移約束:任何兩個連續的狀態元組都是按照狀態轉移函數轉變的。
總的來說,這些約束被稱為代數中間表示法(AIR) 。高級STARK 可以定義更多的約束類型,以處理內存或一個週期內寄存器的一致性問題。
通常意義上的插值意味著找到一個通過一組數據點的多項式。在STARK 編譯流程的背景下,插值意味著找到一個通過多項式表示的算術化約束系統。由此產生的對像不是一個算術化約束系統,而是一個抽象的協議,稱為多項式交互式預言機證明( IOP) 。
常規證明系統中的證明者向驗證者發送消息。但是當驗證者被禁止閱讀這些信息時,會發生什麼?具體來說,如果來自證明者的信息被預言機所取代,那麼該協議就是一個交互式預言機證明(IOP)。交互式預言機可以被看作是一個抽象的黑盒子,通過它,驗證者可以在他選擇的點上進行查詢。當預言機對應於低度的多項式時,它就是一個多項式IOP。顯而易見的是,誠實的證明者擁有一個所有方程都成立的多項式約束系統,而不誠實、作弊的證明者雖然擁有的一個多項式約束系統,但是其中至少有一個方程是錯誤的。當兩個多項式相等時,它們在任何地方都是相等的,特別是在驗證者任意選擇的隨機點上。但是當兩個多項式不相等時,它們幾乎在任何地方都不相等(譯者註:兩個度相同且為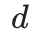 的不同多項式最多只有
的不同多項式最多只有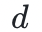 個交點,那麼只要選點範圍足夠大,它們兩就幾乎在任何地方都不相等),當驗證者在隨機點上進行檢驗時,這種不相等就會大概率地暴露出來。
個交點,那麼只要選點範圍足夠大,它們兩就幾乎在任何地方都不相等),當驗證者在隨機點上進行檢驗時,這種不相等就會大概率地暴露出來。
STARK 證明系統插值了代數執行軌跡——也就是說,它找到w 個多項式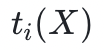 ,使
,使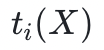 在域D上的值等於代數執行軌跡第
在域D上的值等於代數執行軌跡第 個寄存器的代數執行軌跡。這些多項式被作為預言機發送給驗證者。此時,利用AIR 約束進行多項式操作:將軌跡多項式轉變為商式(只有當軌跡多項式滿足AIR 約束且為低度多項式時,商式才同樣也是一個低度多項式),驗證者模擬這些操作,可以得出這樣新的多項式,其低度證明了約束系統的可滿足性(存在正確解),從而證明了計算的完整性。換句話說,插值步驟將算術化約束系統的可滿足性轉變為對某些多項式低度的要求。
個寄存器的代數執行軌跡。這些多項式被作為預言機發送給驗證者。此時,利用AIR 約束進行多項式操作:將軌跡多項式轉變為商式(只有當軌跡多項式滿足AIR 約束且為低度多項式時,商式才同樣也是一個低度多項式),驗證者模擬這些操作,可以得出這樣新的多項式,其低度證明了約束系統的可滿足性(存在正確解),從而證明了計算的完整性。換句話說,插值步驟將算術化約束系統的可滿足性轉變為對某些多項式低度的要求。
在現實世界中,多項式預言機並不存在。想要使用多項式IOP 作為中間階段的協議,設計者必須找到一種方法來“承諾”( commit )一個多項式,然後在驗證者選擇的一個點上“打開”( open)該多項式(指計算Merkle 樹中一個指定葉子的認證路徑,即向驗證者展示此點之前“承諾”的值)。 FRI 是STARK 證明的一個關鍵組成部分,它實現了上述任務,它通過使用Reed-Solomon 編碼的Merkle 樹來證明多項式的度的有界性。
Reed-Solomon 編碼與多項式 相關(其中
相關(其中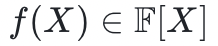 ),是在一個給定域D上的取值列表(其中
),是在一個給定域D上的取值列表(其中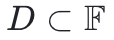 )。在一般的情況下,域D中的元素個數大於多項式允許的最大度數。這些值可以被放入Merkle 樹中,在此場景中,Merkle 樹的樹根可以看作是對此多項式的一個“承諾”。快速里德-所羅門碼接近交互預言機證明(FRI,The Fast Reed-Solomon IOP of Proximity)是一個協議,在該協議中,證明者發送一個Merkle 根的序列,每個Merkle 根對應於一個編碼(編碼的長度在每次迭代後減半)。驗證者檢查連續幾次迭代的Merkle 樹(具體而言:要求證明者提供指定的葉子和它們的認證路徑),以測試一個簡單的線性關係。對於誠實的證明者,提交的多項式的度數每經過一輪就會減半一次,因此遠遠小於碼字的長度。然而,對於惡意證明者來說,這個度數只比碼字的長度小1。在最後一步,證明者發送一個不簡單的碼字,對應一個常數多項式。
)。在一般的情況下,域D中的元素個數大於多項式允許的最大度數。這些值可以被放入Merkle 樹中,在此場景中,Merkle 樹的樹根可以看作是對此多項式的一個“承諾”。快速里德-所羅門碼接近交互預言機證明(FRI,The Fast Reed-Solomon IOP of Proximity)是一個協議,在該協議中,證明者發送一個Merkle 根的序列,每個Merkle 根對應於一個編碼(編碼的長度在每次迭代後減半)。驗證者檢查連續幾次迭代的Merkle 樹(具體而言:要求證明者提供指定的葉子和它們的認證路徑),以測試一個簡單的線性關係。對於誠實的證明者,提交的多項式的度數每經過一輪就會減半一次,因此遠遠小於碼字的長度。然而,對於惡意證明者來說,這個度數只比碼字的長度小1。在最後一步,證明者發送一個不簡單的碼字,對應一個常數多項式。
有一個小問題是上述描述中沒有涉及的:驗證者如何在一個不屬於該域的點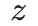 上查詢“承諾”多項式
上查詢“承諾”多項式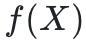 的值呢?原則上,有一個顯而易見的解決方案:驗證者將
的值呢?原則上,有一個顯而易見的解決方案:驗證者將 發送給證明者,而證明者則通過發送
發送給證明者,而證明者則通過發送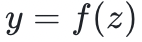 來回應。多項式
來回應。多項式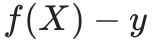 在
在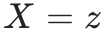 處等於零,所以多項式
處等於零,所以多項式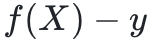 一定能被
一定能被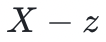 整除。因此,驗證者和證明者都可以獲得一個新的低度多項式:
整除。因此,驗證者和證明者都可以獲得一個新的低度多項式: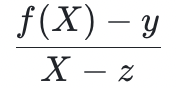 。如果證明者在
。如果證明者在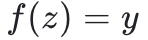 上說謊(即
上說謊(即 ) ,那麼他就沒有能力證明
) ,那麼他就沒有能力證明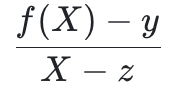 的低度性。所以他的欺詐行為將在FRI 協議的過程中被揭露。事實上,這正是邊界約束(boundary constraints)實施的機制;一個略微複雜但類似的結構可於狀態轉移約束( transition constraints ) 。新的多項式是除掉(約掉)已知因子的結果,所以它們將被稱為商式,表示為
的低度性。所以他的欺詐行為將在FRI 協議的過程中被揭露。事實上,這正是邊界約束(boundary constraints)實施的機制;一個略微複雜但類似的結構可於狀態轉移約束( transition constraints ) 。新的多項式是除掉(約掉)已知因子的結果,所以它們將被稱為商式,表示為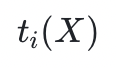 。
。
可見,經過上述流程,多項式IOP 已經被編譯成一個交互式具體證明系統。原則上,該協議可以被執行使用。然而,再做一步密碼學編譯是值得的:用偽隨機(同時也是確定的)代替驗證者的隨機選擇。這正是Fiat-Shamir 變換,經過變換得到是被稱為STARK 的非交互式證明。
上述描述忽略了許多細節問題。本教程的剩餘部分將用更具體、可感的術語來解釋,並將在圖中加入更細節的內容和步驟。
zCloak Network 是基於波卡生態的隱私計算服務平台,使用zk-STARK 虛擬機為通用計算進行零知識證明的生成與驗證。基於獨創的自主權數據和自證明計算技術,可以讓用戶在無需對外發送數據的情況下,實現對數據的分析和計算。通過波卡跨鏈消息傳遞機制,可以為波卡生態內的其它平行鏈以及其它公鏈提供數據隱私保護支持。項目會採用“零知識證明即服務”的商業模式,打造一站式的多鏈隱私計算基礎設施。
原文出自《Anatomy of a STARK》系列,原文鏈接:https://aszepieniec.github.io/stark-anatomy/overview
轉載請註明原文與本文出處及翻譯團隊zCloak Network

















