DAOrayaki DAO研究獎金池:
資助地址: DAOrayaki.eth
投票進展:DAO Reviewer 2/0 通過
賞金總量:75 USD
研究種類:NFT
原文作者: Jonathan W., Vincent H., and Yi Sun
創作者:Skyhigh Feng@DAOrayaki.org
審核者:DAoctor, Yofu@DAOrayaki.org
原文: zkPairing: zkSNARKs for Elliptic Curve Pairings
作者
配對是許多加密協議的核心組成部分。本文我們介紹circom-pairing1,一種在Circom 用於橢圓曲線配對的zkSNARK 電路的概念驗證實現。
簡介
基於配對的密碼學(Pairing-based cryptography2) (PBC)建立在一個叫做橢圓曲線配對(elliptic curve pairing3)的數學對象存在的橢圓曲線密碼學(elliptic curve cryptography4)之上。雖然配對的定義相對複雜,但它們是零知識密碼學現代發展的許多加密對象的基礎: BLS 數字簽名、 KZG 多項式承諾和zkSNARKs。
由於ZK 生態系統中的這個關鍵角色,在zkSNARKs 中實現配對極大地擴展了可尋址密碼構造的範圍,並增加了SNARKs 的反射能力。特別是,我們設想的應用程序的ZK 身份(ZK Identity5) ,區塊鏈擴容,和可編程的SNARKs 。最後的“解鎖”可能會帶來一個未來,任何人都可以在運行中自由組合和聯合不同的SNARKs 。
由於配對涉及許多複雜的橢圓曲線操作,在zkSNARK 中實現它們會帶來許多挑戰。首先,對於非自然域上的橢圓曲線算法,我們必須使用zk-ECDSA6 的大整數和ECC 優化,但是要適應我們的曲線和BLS12-381的配對涉及到在域擴展上操作的事實。其次,Miller 的計算配對算法Miller's algorithm7允許在標準計算模型中進行許多優化,我們將這些優化移植到zkSNARK 設置中。最後,由於配對計算的複雜性,即使最終優化的電路也可能相當大,這意味著需要一些基礎設施的最佳實踐來適應 Circom 工具棧。
在這一系列的文章中,我們提出了一個在BLS12-381曲線上的最優Ate 配對的概念驗證Circom 實現,以及一個在BLS 簽名驗證中的應用實例。然後,我們概述了其他潛在的應用,如遞歸SNARK 和多項式承諾驗證,我們認為這種方法很容易推廣應用。
循環配對
我們實現了循環配對circom-pairing8 代碼庫,它為BLS12-3819 曲線上的以下操作提供未經審核的ZK 電路:
- Tate 配對是最簡單的橢圓曲線配對之一。該算法滿足雙線性特性,適用於密碼學領域,對橢圓曲線的計算和算法的正確實現起到了很好的檢驗作用。
- 最佳配對:最佳配對是實踐中最常用的配對。計算類似於Tate配對(使用Miller的算法,我們將在以後的文章中討論) ; 然而,涉及的步驟較少,而每一步的算法更加複雜,最終的結果是一個較短的總計算。
- BLS10 簽名驗證(短公鑰) : 簽名驗證允許檢查一個BLS 簽名. 給定簽名s,生成元G,公鑰xG,和哈希hash ,驗證電路轉換hash 到橢圓曲線點H(m), 使用maptoG2下面的電路,然後驗證s 確實是由給定的公鑰和消息生成的簽名。 BLS 簽名驗證涉及到評估兩個最優的Ate 配對來驗證這一點e(s,G) = e(H(m), xG) , e 表示最佳的Ate 配對
- 散列hash到曲線: maptoG2 的BLS 簽名驗證操作通過計算橢圓曲線上的點對。正在簽名的消息必須首先散列成一個數值。然後,這個散列值被轉換成橢圓曲線上的一個點; 散列到曲線電路執行這種轉換。
更詳細的文件,我們的電路在這裡可用。這些電路沒有經過審核,也不打算用作生產級應用的庫。
演示
為了說明我們的電路,我們在zkpairing.xyz11 實現了一個演示,它允許用戶生成任何BLS 簽名(以特定的輸入格式)有效性的證明。如果用戶沒有一個特定的BLS 簽名他們可以指定以太坊信標鏈上的任何塊號,並且演示會將塊數據解析為適當的格式,並生成一個驗證該驗證者簽名的證明區塊。對於每個證明,我們提供所有的數據-在三個小文件中-任何人都可以用來在自己的計算機上驗證證明!
基準
所有基準測試都運行在32核3.1 GHz、256G RAM、1T 硬盤和400G 交換機(AWS r5.8 xlarge 實例)上。
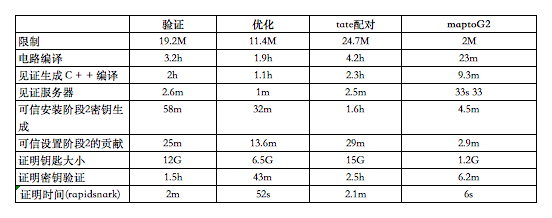
運行大型電路
請注意,驗證和Tate 配對是非常大的電路,因此它們需要特殊的硬件和設置來運行。特別是,必須使用C++ 生成見證服務器,使用rapidsnark 進行證明,使用補丁版本的Node.js而不使用垃圾收集生成密鑰。所有這些都必須在具有大容量內存的機器上完成; 我們的設置工作流程在《大電路最佳實踐》( Best Practices for Large Circuits12 )文檔中有詳細說明。
我們能用zkPairing 做什麼?
因為配對是許多加密協議的核心組成部分,所以用於配對計算的zkSNARKs 允許我們將以下高級原語放入SNARK 中:
- BLS 簽名驗證: Boneh-Lynn-Shacham (BLS)數字簽名是一種基於橢圓曲線配對的簽名方案。由於能夠使用BLS 有效地計算聚合簽名和閾值簽名,它目前被用於區塊鏈,如Etherum 2.0、 ZCash 和 Dfinity 。驗證BLS 簽名涉及到一個配對檢查,檢查兩個橢圓曲線配對是否相等,因此通過zkPairing 直接啟用。這解鎖了潛在的可伸縮應用程序,比如輕型客戶機和橋接的簽名聚合。
- 遞歸SNARK 驗證: 因為Groth16證明驗證只涉及配對檢查,所以SNARK-ing 配對允許SNARK-ing 整個驗證算法,稱為遞歸驗證。這使我們能夠構建一個zkSNARK 的zkSNARK 的... 無限廣告,使開發人員能夠構建不同的SNARK 證明,而不是構建一個單一的大型SNARK 和大大增加可能的SNARK 的複雜性。我們正在調整我們的電路,以遞歸Groth16驗證BN254,並希望在不久的將來發布一個概念證明。
- KZG 多項式承諾驗證: KZG 多項式承諾是PlonK 的基礎,PlonK 是具有通用可信設置的新一代zkSNARK 之一。因為驗證KZG 承諾涉及到一個配對檢查,zkSNARK-ing 配對使我們能夠驗證任何建立在SNARK 中的KZG 承諾之上的東西,包括PlonK 驗證本身!
很快就會看到第2部分討論了zkPairing 的實現技術!
致謝
該項目是在ZKxZK Gitcoin 基金的支持下,在0xPARC 的ZK 身份工作組期間構建的。
我們藉鑑並分享了很多與circom-ecdsa 相關的技術,特別是在大整數和橢圓曲線算法的優化方面。例如,我們使用xJsnark 的大整數乘法優化。
我們也從最初的創作者Jordi Baylina 和snarkjs 的研究中獲益匪淺。他教了我們很多關於circom/snarkJS 工具棧的知識,並分享了很多關於如何有效地構建大型ZK 電路的見解。
參考
- https://github.com/yi-sun/circom-pairing
- https://en.wikipedia.org/wiki/Pairing-based_cryptography
- https://medium.com/@VitalikButerin/exploring-elliptic-curve-pairings-c73c1864e627
- https://en.wikipedia.org/wiki/Elliptic-curve_cryptography
- https://0xparc.org/blog/zk-id-2
- https://0xparc.org/blog/zk-ecdsa-2
- https://crypto.stanford.edu/pbc/notes/ep/miller.html
- https://github.com/yi-sun/circom-pairing
- https://hackmd.io/@benjaminion/bls12-381
- https://datatracker.ietf.org/doc/html/draft-irtf-cfrg-bls-signature-04
- https://zkpairing.xyz/
- https://hackmd.io/V-7Aal05Tiy-ozmzTGBYPA?view
















