第一章 背景介紹
隨著數字資產量化基金行業的發展,如何構建基金組合的討論日益增多,市場對FOF管理人的專業要求也日趨嚴格。傳統金融市場中的資產配置策略大致可劃分為現代組合理論、風險均衡/平價策略以及等權重組合策略。現代組合理論和風險均衡理論下又有細分。下圖展示了不同理論下的代表性模型:
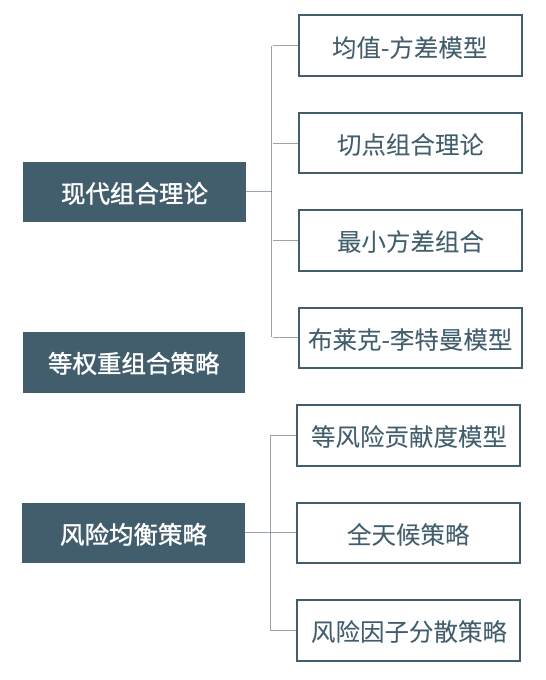
本文將簡述上圖中的策略,討論其在數字資產市場的應用和指導意義,並對不同配置策略進行了歷史回測。另外,如無特別說明,本文中的風險水平均默認表示為收益的方差。
第二章 現代組合理論
現代組合理論是資產配置中最常見的配置策略。現代組合理論認為,一個有效組合是在給定風險水平下最大化期望收益率而得到的資產組合,又叫做“均值-方差”模型。最優資產組合併不是單一的,而是由一系列最有組合構成,從而形成所謂的“有效前沿”。從數學角度,對於一個具有n種資產的域,“有效前沿”的計算可以轉換為二次優化問題:
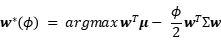
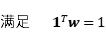
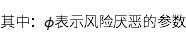


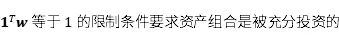
(一) 切點組合理論
托賓在1958年指出,在存在無風險資產的情況下,存在一個優於其他所有資產組合的最優組合。定義r為無風險資產的收益率。在期望收益率和標準差的坐標系中,從(0,r)出發、與“有效前沿”相切的線,被稱為資本市場線(capital market line),資本市場線與“有效前沿”相切的組合優於其他所有的風險資產組合,被稱為切點組合。可以發現,切點組合也就是使得夏普比率最大化的風險資產組合。
目前數字資產市場尚無所謂的無風險利率,因此不存在資本市場線。本文所有夏普比率的計算中均規定無風險利率為0,因此預期收益/標準差即為夏普比率。據此,“有效前沿”中最大化預期收益/標準差的點與切點組合的定義類似,因此看作為切點組合理論下的資產組合。根據定義,切點組合為“有效前沿”上的一點,因此切點組合理論隸屬於現代組合理論。下文中切點組合理將作為現代組合理論的代表,與其他配置策略進行比較。
(二) 最小方差(MV)組合
有很多方法可以用來獲得激進程度較低的積極型投資組合。其中最直接的方法就是採用較低激進性的參數。例如,不再基於歷史數據對未來收益率進行預測,而是假設所有資產的期望收益率都相等。在這個假設下,最優資產組合也就是最小化波動率的結果,又稱最小方差(MV)組合。實際上,最小方差組合即上述計算“有效前沿”的二次優化問題,當
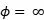
時的解。最小方差組合的求解可以轉化為二次優化問題:
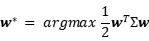
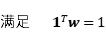
(三) 布萊克-李特曼模型
布萊克-李特曼模型在現代組合理論的基礎上引入了組合管理人的個人判斷,即將管理人的個人判斷和市場上的歷史信息結合起來,並根據管理人對自己主觀判斷的信心程度,得到對資產的預期收益和協方差矩陣,是一種典型的貝葉斯分析方法。
布萊克-李特曼模型以市場均衡(即市場需求和供給相等的狀態)情況下的資產比例為起點。通常情況下,我們認為市場本身永遠是均衡的,那麼當前市場上資產的比例也就是市場均衡下的比例。於是可以從市場比例,通過倒推優化方法得出隱含均衡期望收益率的估計值。管理人對資產不同於隱含均衡收益率的觀點,配合對其觀點的信心程度,將最終決定模型對資產預期收益和資產間協方差矩陣的最終估算。而後依據現代組合理論,得到給定風險水平下最大化期望收益率的資產配置權重。定性地說,管理人對某資產相對於隱含均衡收益率的判斷越正面,信心程度越高,該資產得到的權重越大。
對於傳統市場中的資產管理來說,布萊克-李特曼模型主要有以下兩方面優點:
1. 通過把市場均衡引入模型,得出的權重更加分散的同時更具實際意義;
2. 通過把管理人的主觀觀點量化並引入模型,為主觀判斷結合市場歷史信息的配置策略提供了很好的框架,使得模型更為實用。
然而,上述優點同樣是布萊克-李特曼模型應用在數字資產量化FOF的限制所在。首先,基於市場均衡的假設,布萊克-李特曼模型對配置權重在市值權重的基礎上進行調整。由於數字資產市場尤其是量化基金領域仍處於發展初期,存在市場信息不對稱、合規機制不完善等諸多問題,均衡市場的假設很難成立。基金的管理規模很大程度上不是市場選擇的結果,因此基於市值權重的布萊克-李特曼模型難有說服力。其次,主觀觀點的量化過程存在一定難度。布萊克-李特曼模型主要應用於大類資產的戰略配置中,傳統市場中對大類資產的研究體系已十分成熟並有長周期的數據支持,因此主觀觀點的量化過程已有章可循、相對簡單。而在數字資產量化基金領域,針對量化產品研究尚處於起步階段、沒有被業界廣泛認可的成熟體系,基金產品的存續時間普遍較短缺乏足夠的歷史數據支持,因此主觀觀點的量化過程往往給模型引入更多噪音。
第三章 等權重組合(1/N)策略
降低投資組合激進程度的另一方法是採用資產配置的探索式方法。探索式是指基於經驗技術和試錯方法來尋求可接受的解,這個解並不等同於優化問題的最優解。等權重組合策略就是這種探索式、非最優估算方法下的一個例子。等權重組合即將投資組合中所有資產都設置為等權重,在大大降低輸入參數敏感性的同時解決了現代組合理論中權重分配過於集中的問題。然而,等權重策略不屬於積極型管理的範疇,完全忽略市場信息,在此不作更多討論。
第四章 風險均衡策略
相較於現代組合理論,風險均衡策略需要更少的輸入參數、是探索式方法下的又一例子。風險均衡策略又稱為風險平價策略,均指risk parity模型,只是翻譯不同。一般情況下,風險均衡策略目前有三個層面:針對風險貢獻度的均衡、針對風險情景的均衡和針對風險因子的均衡。這三種均衡屬遞進關係,越來越接近真正的風險分散。
(一) 等風險貢獻(ERC)模型
針對風險貢獻度的均衡策略通過賦予不同資產以相等的風險貢獻度來構造一個平衡型的投資組合,因此又被稱為等風險貢獻(ERC)模型。假設資產收益率符合正態分佈:
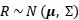
對於權重為
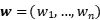
的資產組合,其標準差為:
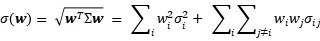
定義資產i的的邊際風險
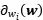
即資產i的配置權重wi的增長引起的組合風險的增長為:
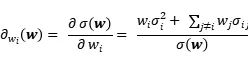
於是,資產i對組合的總風險貢獻為:
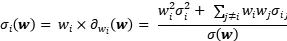
從數學角度,風險均衡策略可以轉化為下述問題:
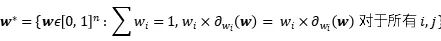
以五支子基金構成的投資域為例,風險均衡策略下的配置方案如下:
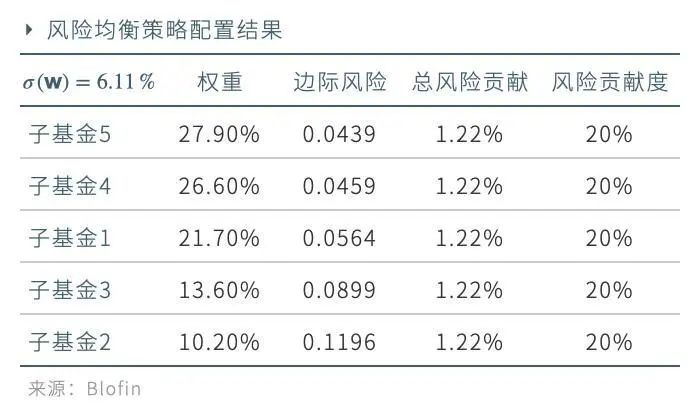
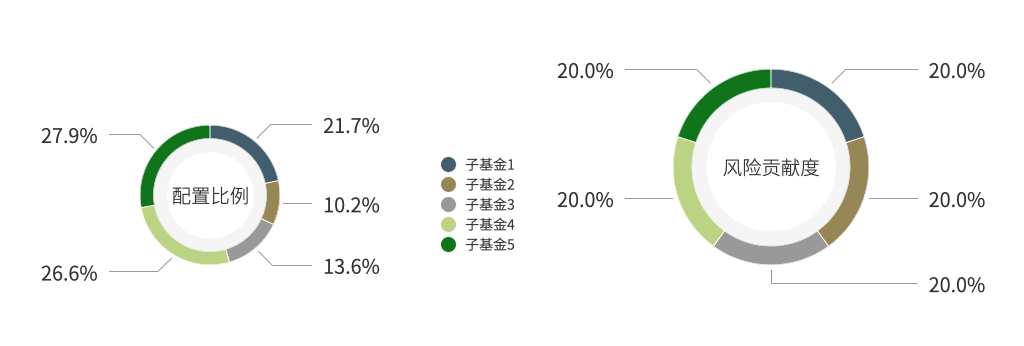
(二) 全天候(All Weather)策略
橋水基金提出的全天候策略是針對風險情景均衡的例子。簡單來說,全天候策略認為各類資產價格的波動是由於預期差,並使用影響大類資產走勢的最核心變量經濟增長和通脹兩個維度區分預期差。從超出市場預期和低於市場預期的角度、增長和通脹兩個維度區分得到四個不同象限,在每個像限中,都會有資產因為預期差而表現較好。全天候策略就是通過調整受益於各預期差的資產的配置比例實現對每一個預期差的均衡配置。
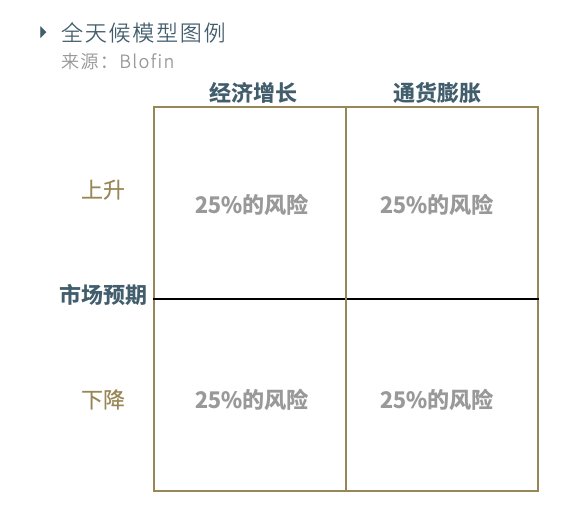
雖然在大類資產配置中表現亮眼,全天候策略在數字資產FOF管理中的應用尚且有限。對基金產品的分類和影響基金表現的核心變量的研究要求較高,是Blofin未來研究的方向之一。
(三) 風險因子的分散策略
丹麥養老金管理機構ATP採用的風險因子分散策略在業內處於領先地位。 ATP將風險均衡的對像從資產轉向因子,並開創性地將風險因子概括為利率因子、通脹因子、股票因子和其他因子。根據基於因子和資產的映射關係調整資產的配置比例以實現對各類風險因子的暴露均衡。
相較於資產,因子是更加底層、相互更加獨立的收益和風險來源。傳統市場中FOF管理從資產的配置轉向風險因子的配置已成趨勢。數字資產市場起步較晚,尚無針對數字資產的風險因子體系,短期內FOF實現風險因子的均衡配置有一定難度。 Blofin作為專業的FOF管理和研究機構,未來將致力於數字資產量化行業內的風險因子體系的搭建。
第五章 歷史回測
本節將以五支典型的數字資產量化基金組成的擬投資產域為例,比較前文所述的不同策略的配置結果。為公平進行比較,我們統一用五支子基金2019.11.1至2020.2.29的淨值數據作為訓練集計算配置方案。根據訓練期各基金的淨值標新預測得到收益與協方差矩陣(可由表中波動率及相關性矩陣得到)如下表所示:
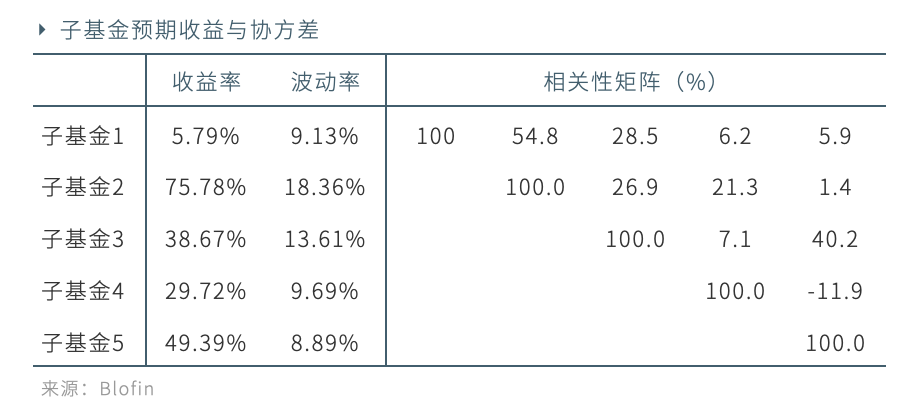
各策略得到的權重分配如下圖所示:
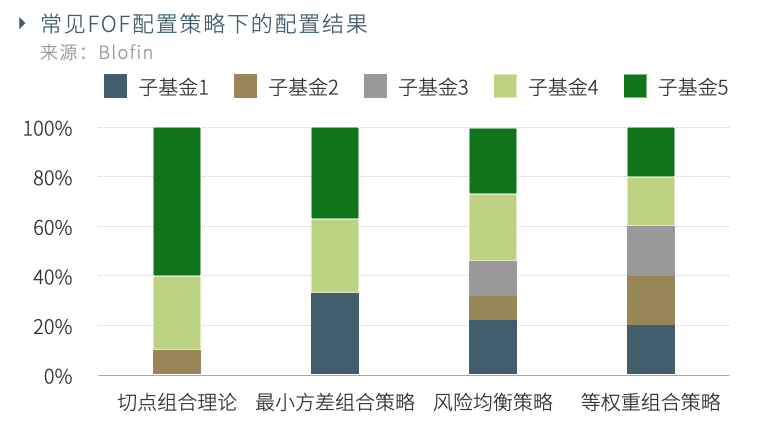
可以看出,現代組合理論中切點組合理論和最小方差組合理論均配置了三支基金,權重分配相對集中。特別是切點組合理論,分配給單只基金(子基金5)的權重超過了50%。由於子基金2自身的波動率高且與其他子基金的相關性較高,風險均衡策略分配給子基金2的權重較少。相較於大類資產波動率差異的明顯,數字資產量化基金則走勢相似,具體表現為:即使是不同策略的基金,它們的波動率依然落在同一量級。這導致風險均衡策略下的權重結果並未能與等權重策略有明顯區分。
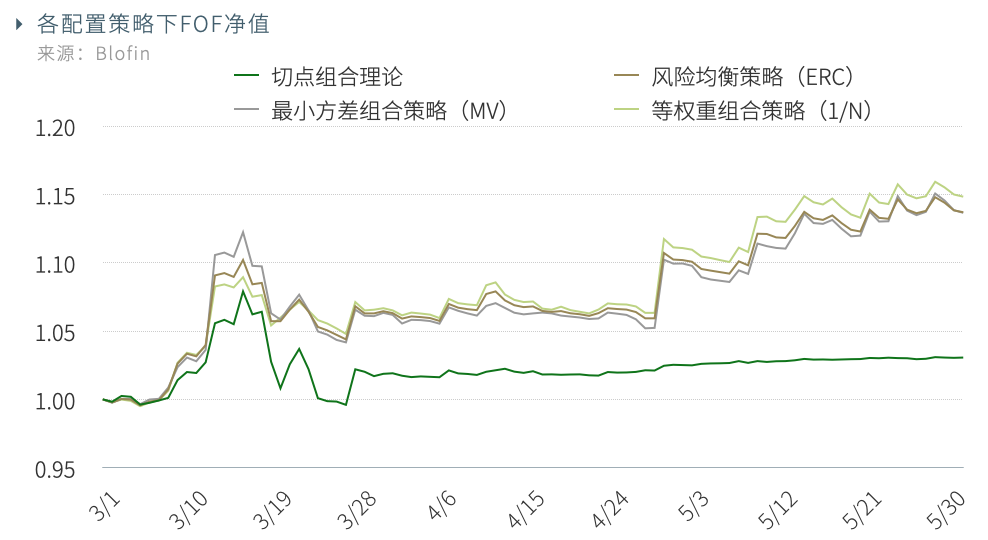
不同配置策略下的FOF在2020.3.1到2020.6.1的淨值回測結果如下圖所示:
各策略下FOF的表現如下表:
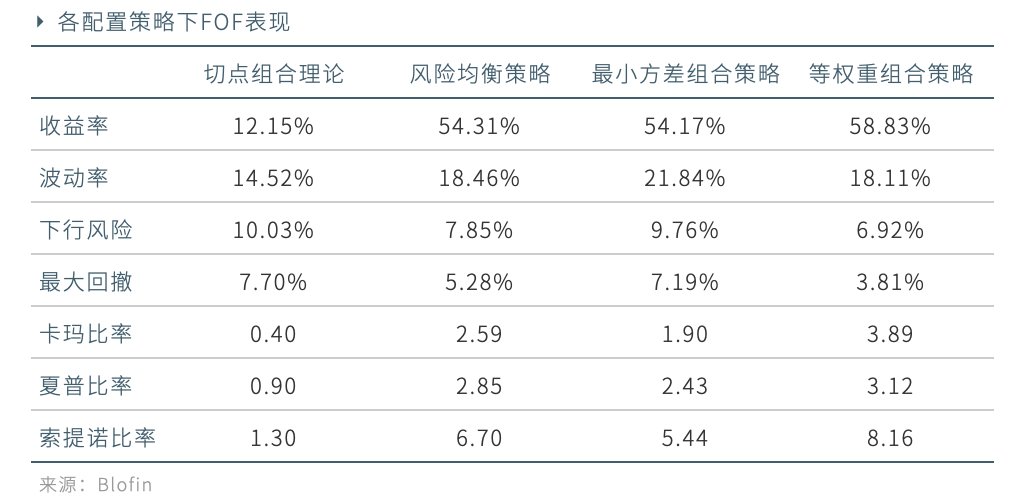
測試週期跨越了312大跌、比特幣第三次區塊獎勵減半等行情。由於訓練集時間跨度有限,對基金未來收益率和協方差矩陣進行估計預測又完全基於歷史數據的現代組合理論劣勢明顯。复盤來看,子基金5在訓練週期(2019.11.1至2020.2.29)表現亮眼,但測試週期(2020.3.1到2020.6.1)的表現十分不理想,出現了較大回撤。由於切點組合理論對歷史數據最為敏感,當資產在測試期和訓練期的表現差異擴大時,切點組合理論的結果現會明顯偏離預期。與等權重組合策略相比,風險均衡策略並未表現出明顯優勢,原因可能是回測週期較短並且子基金間的波動率差異有限。
第六章 各配置策略的探討和優化
在現代組合理論的資產配置邏輯通俗易懂,模型簡單易用,因此曾在傳統金融市場被廣泛使用。然而,互聯網危機以來,學術界和業界對現代組合理論的質疑和批評越來越多,主要集中在以下方面:
1. 現代組合理論的運用要求對協方差矩陣進行估算、並且要預測資產的未來收益,最優資產組合對這些輸入變量非常敏感。輸入變量的細微調整將導致計算所得最優權重向量w* 發生很大變化,穩定性較差。
2.對協方差矩陣和未來收益的估算預測往往依賴長期歷史數據,認為歷史數據可以給出未來發展的可靠方向。但是,在極端行情下,資產間的相關性急劇上升,根據歷史數據估算所得的協方差矩陣很難給出理想的分散風險的效果。
由於數字資產量化行業的歷史數據相較於傳統資產還十分有限,基於歷史數據的對協方差矩陣和未來收益的預測顯得缺乏說服力,加劇了現代組合理論應用在數字資產FOF管理中的局限性。
3.根據現代組合理論得出的最優組合普遍存在過度集中於某幾類資產的情況。下表比較了根據現代組合理論和其他常見配置策略得到的資產配置結果:
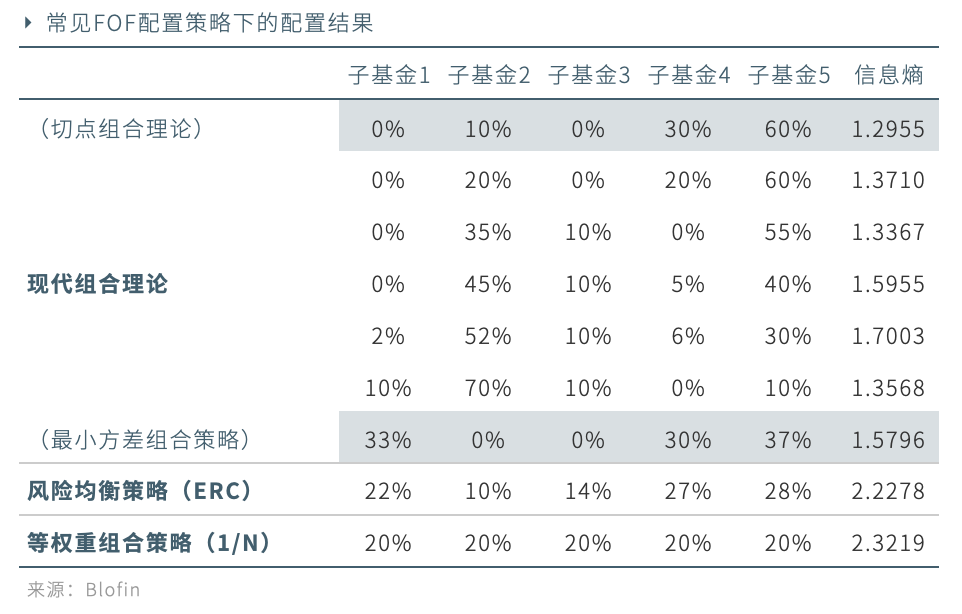
從上表可以很直觀地感受到現代組合理論下的權重分配最為集中。最後一列中的信息熵是表徵離散程度的指標,熵越大則表示權重分配的集中程度越低。現代組合理論下的信息熵明顯小於其他策略。
上述問題可以通過收縮法和正則化技術得到有效改善。兩種方法的思路均為優化資產間協方差矩陣的估算過程。收縮法通過引入權重約束而間接改變了協方差矩陣,相當於在歷史數據的基礎上引入了組合管理人的一些判斷,與下文中提到的布萊克-李特曼模型屬於同一類。正則化技術則是將不同的協方差矩陣參數估計值加以綜合,從而平穩最優組合的權重。正則化技術或是收縮法只是降低了參數值的激進程度,並沒能減少輸入參數的數量。現代組合理論對輸入參數的高敏感性是客觀存在的,在投資管理中屬於激進型模型。
風險均衡策略則相對保守,其實質是通過風險分散和對沖,實現組合穿越週期的目標,也確實從很大程度上克服了現代組合理論中的問題。然而,風險和收益是資產管理天坪的兩端,是資產管理需要處理的核心矛盾。專注於風險管理的配置策略自然疏忽了投資人對收益的要求,且對低波動率資產配置比例過高,是風險均衡策略的主要弊端。槓桿的引入解決了這些問題。隨著數字資產借貸市場和衍生品市場的不斷發展,風險均衡策略在FOF管理中的應用將更為靈活以滿足不同投資者偏好。
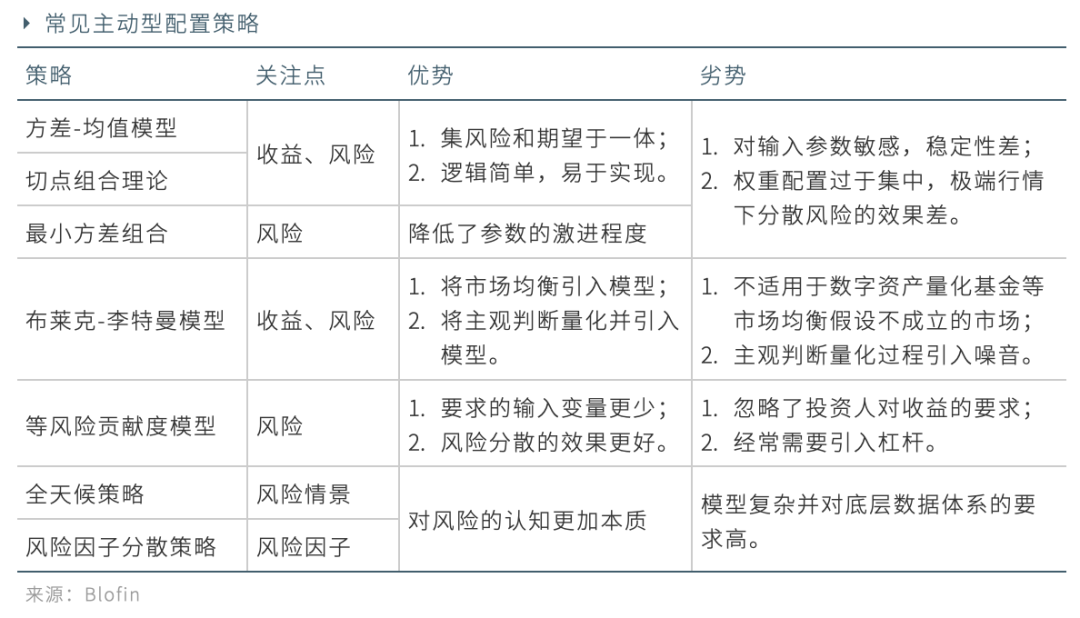
下表總結了各主動型策略的特點以供參考:
第七章 總結與展望
作為新興的數字資產量化行業,在經歷了早期的野蠻成長期之後,逐漸向運營合規化、管理正規化和收益合理化的方向轉變。而以數字資產量化基金作為投資標的的FOF基金,憑藉其專業的投資和管理能力,也越來越受到投資者的認可。
然而,數字資產量化FOF投資還處於早期,尚無成熟的經驗可循,資產配置的方法論也不完善。而傳統投資市場成熟完善的配置理論和方法,對於數字資產量化FOF的資產配置,有很強的借鑒意義。通過比較研究,我們發現:在諸多的資產配置理論中,現代組合理論邏輯簡單易於實現,但存在對輸入參數敏感、穩定性較差的問題;針對風險貢獻的均衡模型大大降低了對輸入參數的要求,然而需要引入槓桿以滿足不同的收益要求;針對風險情景和風險因子的均衡策略對風險的認識更加本質,模型也更為複雜,需要更多體系化數據和分析手段的支持。
當前,由於缺乏必要的底層設施(如合規機制、風險因子體系),傳統市場上的諸多配置策略應用於數字資產市場的難度較大。對於目前可用的策略,由於歷史週期較短,不同策略的回測結果差異性有限,還有待更多歷史週期的檢驗。 Blofin在積累數據的同時,將繼續致力於對數字資產市場尤其是量化基金的體系化研究和基礎設施的完善。

















