編者註:本文為EthWorks 撰寫的一份關於零知識證明和區塊鏈擴展方案關係的報告;對可擴展性問題、零知識證明和ZK rollup 擴展方案都做了簡潔的介紹。本譯稿的校對得到了安比實驗室的大力支持,他們對原報告解釋不足及有所疏漏的地方做了相當多的說明(後文括號以“安比按” 開頭的文段即他們補充的內容)。在此對他們致以誠摯的謝意。
1. 引言
1.1 可擴展性問題
你可能已經很了解區塊鏈的歷史了(但我還是多廢話一下)。 2017 年,比特幣開始登上主流媒體的頭版頭條,激起了前所未有的關注,全球人民都看到了該技術所面臨的挑戰。隨著比特幣日趨流行,比特幣交易亦大量發生,網絡擁堵達到了前所未有的程度。交易手續費的暴漲使得比特幣轉賬變得脫離實際。最近,以太坊也顯露出了同樣的問題。相比低峰時期,以太坊上的礦工費(Gas Fee)已經增長了30 至50 倍。
所有這些現象反映出的問題是整個社區早就心知肚明的:比特幣區塊鏈的初始設計並不適合大規模普及。由於比特幣每秒的最大交易處理量只有數筆,遠遠比不上Visa 或PayPal 等主流支付網絡。我們通常將這個局限性稱為區塊鏈可擴展性問題。
以太坊的目的是比比特幣更快地確認交易,但是遠不足以解決這個問題。以太坊的交易吞吐量—— 高於比特幣,但是每秒交易處理量只有十數筆—— 還不足以讓該網絡實現大規模採用。以太坊也會出現擁堵情況,即使是很簡單的智能合約操作也需要花費數美元。
邊注:區塊鏈的實際吞吐量
鑑於比特幣的設計,其交易吞吐量從理論上來說只有每秒7 筆。實際上,由於空塊、複雜的輸入和輸出交易等問題,吞吐量平均只有每秒3 筆。當比特幣網絡於2017 年通過軟分叉更新隔離見證協議後,吞吐量增至4.6 筆,還是連每秒7 筆都達不到。
同樣地,以太坊的設計交易吞吐量是每秒15 筆。不過,這個限制是動態變化的(取決於礦工所設定的區塊Gas Limit)。假設當前網絡將區塊的Gas 上限設為1200 萬,實際吞吐量將達到每秒36 筆以上。但是,這一推論僅適合於區塊中只有以太幣轉賬交易的情形,因為代幣轉賬的成本要高出2.5 倍,更別提與智能合約進行更複雜的交互了—— 其成本通常會高得多。
在區塊鏈行業,已經有許多可擴展性項目慘遭失敗。還有的項目僅僅停留在白皮書階段,或削足適履、扭曲區塊鏈的內涵來騙取關注。我們有理由認為,可擴展性問題沒有最終的解決方案,新的解決方案總會增加複雜性和難度。
即使我們接受了這個事實,過去幾年間可擴展方案領域的進展仍然令人沮喪。但是,黑暗的盡頭是光明,我們即將迎來轉機。
今年早些時候,一位客戶要求我們調查可擴展性方案的市場時,我們似乎聽到了一場革命的號角。最近,幾個前景光明的團隊已經宣布了項目里程碑。以太坊社區又開始躍躍欲試起來。
我們知道,過多的信息可能反而會起誤導作用,讓人難以把握全貌,因此我們決定幫大家梳理一下。通過本文,我們想要分享我們與區塊鏈開發者乃至整個區塊鏈社區進行可擴展性研究所得出的成果。我們相信,本文將幫助大家了解零知識證明和二層可擴展性方案的潛力,同時更深入地理解這些技術。
1.2 報告內容
比起以往,可擴展方案的市場已經有所發展,無數致力於開發此類方案的公司割據一方。面對如此海量的解決方案,我們很容易感到迷失,難以辨別哪些方案最有前景。
因此,我們決定認真分析並比較這些解決方案,找出那些最有潛力的方案、幫助企業家和開發者做出正確選擇。我們主要關注基於零知識證明的二層方案,因為我們發現這些方案具有很高的安全性和相對較短的資金退出時間,因此從長遠角度來看潛力最大。
還有至少兩類前景良好的方案本文沒有涉及:optimistic rollup 和狀態通道。這兩類方案都不是基於零知識證明構建的,因此不在本文的討論範圍內。
邊注:什麼是二層解決方案?
二層可擴展性解決方案的目標是在現有區塊鏈的基礎上增加額外的協議,提高以太坊的最大吞吐量(即,處理交易的速度)並減少終端用戶所需支付的交易費。不同於ETH 2.0 等一層方案,二層方案將基礎協議作為一個去中心化的安全層,然後在上面構建另一層(不改變以太坊的共識算法或其他任何核心概念)。
二層方案將原本由以太坊執行的計算轉移到了鏈下,將以太坊作為安全性保障。由於計算被轉移到了鏈下,需要存儲在鏈上的數據量大幅減少,在降低交易成本的同時加快了交易速度。
2. 零知識證明
2.1 簡介
本文詳細介紹的解決方案使用零知識證明密碼學來確保交易安全性並實現鏈下計算。因此,在深入研究可擴展性解決方案之前,我們需要對零知識證明技術有個基本的了解。
零知識證明(簡稱ZK)是密碼學的分支,是區塊鏈社區近年來追逐的熱點之一。通過零知識證明,一方(證明者)可以向另一方(驗證者)證明他擁有一些知識,但是無需透露知識本身及其它可以用來破解這些知識的信息。證明者只需向驗證者傳達並證明的信息是,他確實擁有這些知識。
聽不懂也沒關係。我們來舉個簡單的零知識證明的例子。
2.2 現實生活中的例子
關於零知識證明是如何運作的,Konstantinos Chalkias 舉過一個絕妙的例子。假設有兩個好朋友Victor 和Peggy,他們都喜歡在雙休日去公園玩雜耍球。 Victor 是紅綠色盲症患者。對他來說,這些球的顏色都一樣。
兩人決定像往常一樣去中央公園(Central Park)玩雜耍球。 Peggy 自己帶了一個紅球和一個綠球。紅綠色盲症患者Victor 無法看出這兩個球的區別。
為了向Victor 證明兩個球的區別,Peggy 讓Victor 一手抓著一個球藏在背後,然後反復交換手中的球。每次交換過後,Victor 都會向Peggy 展示任意一個球,問她這個球是否與上個球不同。
每當Victor 交換過手中的球,Peggy 都能辨別出他展示的球是否與上一次不同,因為她分得清紅色和綠色。這樣一來,Victor 就可以確定Peggy 知道這兩個球的不同,同時他又無法知道這兩個球的顏色。這就是零知識證明。
儘管Peggy 有高達50% 的概率可以猜中一兩次,但是隨著他們重複的次數越多,猜中的概率就會無限趨近於零。因此,Victor 完全可以確定這兩個球的顏色是不同的。
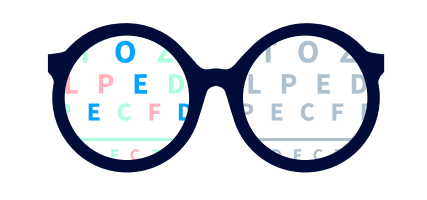
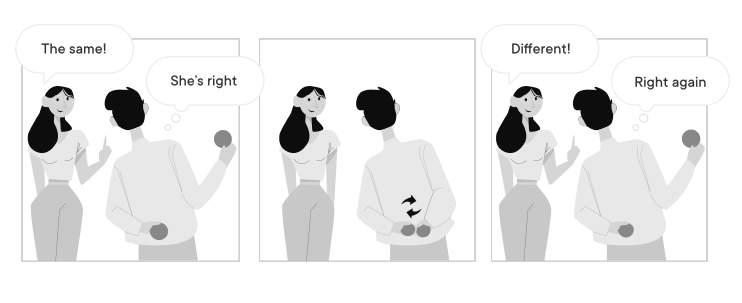
- Vitcor(驗證者)眼中的世界 -
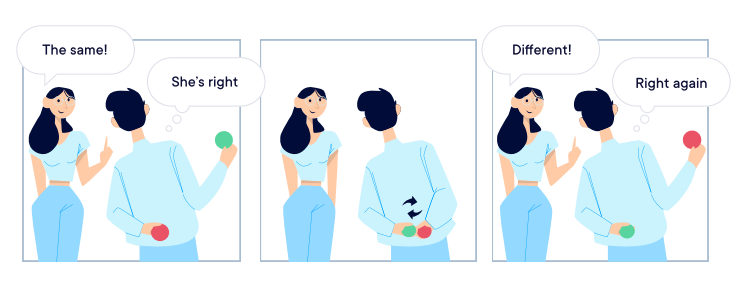
- Peggy(證明者)眼中的世界 -
2.3 零知識證明和區塊鏈
零知識證明可以用來生成關於某個計算已經按照預定規則執行的密碼學證明。這類證明可以用編好的計算機程序來生成,並可以自動驗證。
零知識證明之所以有助於解決可擴展性問題,是因為零知識證明本身比其所代表的數據小得多,零知識證明可以用來實現交易的匿名化。
(安比按:不是所有的零知識證明技術生成的proof 都比statement 小得多。零知識證明技術僅必須滿足三種要求:完備性(completeness)、可靠性(soundness)、零知識性(zero- knowledgeness),並不要求一定要具備這種小體積性。)
邊注:基於零知識證明的可擴展性方案並不會從根本上改變區塊鏈的擴展性,只是改變區塊鏈的用法:小型計算全部從鏈上轉移到鏈下執行,區塊鏈只需驗證大批計算結果即可。
通過二層擴展方案生成的零知識證明首先需要遵守一組預定義規則。如果是交易系統,這組規則可能類似區塊鏈的共識規則,例如,每個交易必需署上正確的簽名,或者用戶不得透支等。二層系統將規則轉化成了一連串數學表達式(電路和多項式),然後使用這些數學表達式來創建零知識證明生成過程所必需的兩個計算機程序:證明者與驗證者。
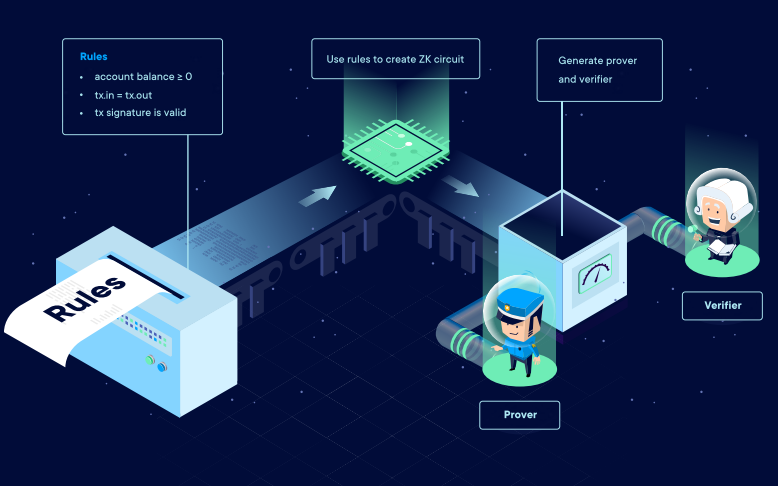
只要有了證明者和驗證者,我們就可以使用該系統生成並驗證交易。假設Alice 的錢包裡有3 ETH ,她想向Bob 轉一筆賬。她簽署了交易,交易數據被提交到了證明者手裡。證明者使用該數據生成了一個零知識證明,然後發送給驗證者。現在讓我們考慮以下兩個場景。
2.3.1 生成一個有效的零知識證明
驗證者可以在完全不知道交易信息的情況下驗證Alice 是否按照預定義規則執行了交易。其中一條規則是Alice 不能透支,因此如果她想轉賬2 ETH ,驗證者會同意該交易。
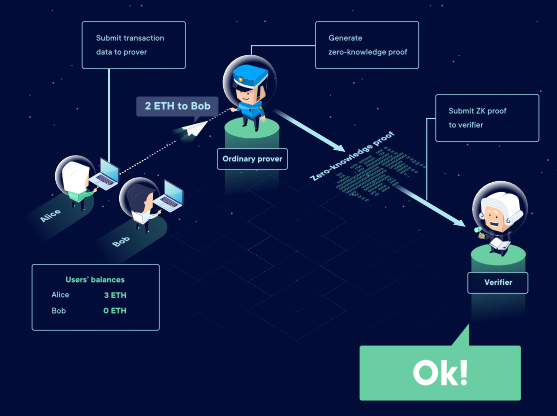
2.3.2 生成一個虛假的零知識證明
現在,假設Alice 想要發送5 ETH 。按理說,該交易在證明者階段就會遭到拒絕。即使證明者作惡,該交易也得不到許可,通不過驗證者的驗證,因為它沒有按照規定執行。
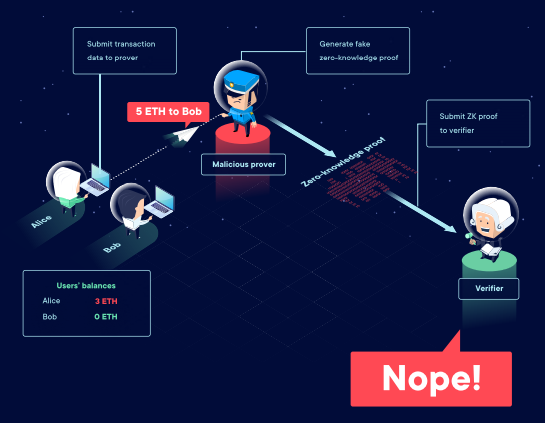
(安比按:讀者應該注意到了,2.3.1 章節和2.3.2 章節分別就是零知識證明屬性中的“完備性” 和“可靠性”:正確的證明必定能夠通過驗證;錯誤的證明必定不能通過驗證。這裡並沒有用到零知識證明的“零知識性”。因此,若不需要滿足隱私要求,僅僅是為了提高可擴展性,則任何滿足完備性、可靠性、簡潔性(證明體積小) 、驗證速度快的證明系統,實際上都能用作同樣的用途。因此,Vitalik 就曾提議“以snarks 替換掉ZK rollup 的ZK 前綴”,或者更細緻的命名比如“Validium”,因為這些方案實際上都沒有用到零知識屬性。包括StakWare 也一直在強調自己是在利用證明系統(proof system)實現計算完整性(computational integrity)證明。但在“ZK rollup” 深入人心的情況下,AZTEC 使用零知識證明(提供隱私性)的rollup 方案,只好命名為“ZK-ZK-rollup”。令人唏噓)
2.4 SNARK vs. STARK
目前為止,已經有很多基於零知識證明的密碼學證明興起,其中最知名的莫過於SNARK 和STARK 。它們之間有著非常重要的聯繫。
SNARK 代表的是:
簡明性(succinct):該證明遠小於其所代表的數據,並且可以迅速驗證。非交互式(non-interactive):證明者只會發送一組信息給驗證者,因此二者之間不需要來回交互。知識論證(argument of knowledge):從計算層面來說,我們認為該證明是完備的—— 惡意證明者無法欺騙系統,除非TA 確實掌握該知識的具體內容,以此支持TA 提出的證明。
(安比按:密碼學中對proof(證明方案)和auguement(論證方案)還有區分。方案的可靠性(soundness)要能達到對抗具備無限大計算資源的證明者,才能稱為proof;而arguement只需能抵禦計算能力為多項式的惡意證明者即可,不需要能抵禦計算能力無窮大的惡意證明者。)
可擴展性解決方案所使用的SNARK 需要在證明者和驗證者之間構建可信初始化(trusted setup)。可信初始化是一組類似遊戲規則的初始公共參數,由一群志願參與者在指定時間執行聯合計算,即,所謂的可信初始化儀式(trusted setup ceremony),來生成。只要有至少一位參與者是誠實的,就能安全地生成參數。因此,參與者人數越多,機制的可信度就越高。
STARK(例如StarkWare 開發的FRI-AIR STARK)不需要可信初始化—— 因此,此處的“T” 代表“透明的(transparent)” 。這就為整個系統排除了單點故障的隱患。雖然STARK 證明的數據量較大,但對大批次的交易可以平攤計算成本。因此,STARK 能夠提高可擴展性。
邊注:就基於早期SNARK 技術(即,Groth16)的解決方案而言,每當Groth16 上線新的版本,都要執行可信初始化儀式。因此,下文所述的Loopring 去年上線最新版本時,也需要執行該機制。 SNARK 還有一種變體稱為通用SNARK(Universal SNARK)或SNORK(例如,PLONK 和SONIC)。該技術使用的是通用可信初始化(universal trusted setup)。例如,zkSync 的創建者無需在上線新版本時執行可信初始化機制:他們復用了去年包括Vitalik 在內的200 多位知名人士一起執行的多方計算的執行結果。通過通用可信初始化,可以擴展或更新協議中所使用的零知識證明方案,而無需執行一個新的儀式。
(安比按:SNORK = Succinct Non-interactive Oecumenical (Universal) aRguments of Knowledge (簡潔的非交互性通用知識論證),實際上就是帶有通用且可升級的可信初始化設置的SNARK。)
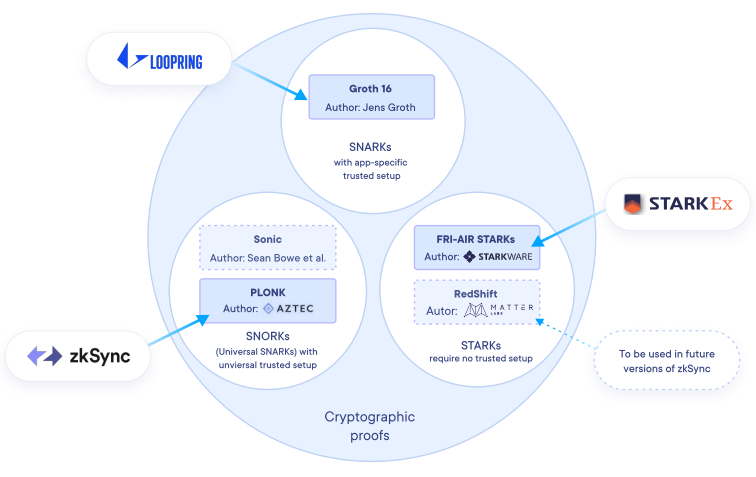
- 不同的密碼學證明方案之間關係的示意圖(來源:Alex Gluchowski) -
3. 架構
本文所述解決方案的共同點是都使用了零知識密碼學。它們之間的差異性則源自數據可用性問題。
3.1 數據可用性問題
用戶餘額相關的交易數據和信息可以存儲在底層區塊鏈上,也可以不存在區塊鏈上,這就要在可擴展性和安全性之間進行基本的權衡取捨。
鏈上存儲數據的安全性類似於直接將資產存儲在以太坊上,而無需用戶執行額外的操作。用戶可以隨時獲取數據。這一點非常重要,尤其是在可擴展性解決方案提供商的服務器被破壞或作惡的情況下。鏈上數據可用性可以讓用戶創建一個證明來證明他們持有一定數量的代幣,無需與二層系統進行交互就可以直接將這些代幣從智能合約中取出。將數據存儲在鏈上的基於零知識證明的解決方案被稱為 zkRollup 。
將數據存儲在鏈下的可擴展性方案引入了數據可用性問題,因此會削弱二層方案的安全性。一旦某個可擴展性解決方案提供商終止合作,普通用戶就無法取出他們的資金,除非他們能獲得代表其餘額的數據。這類解決方案被稱為 Validium 。為了緩解數據可用性問題,這類方案或將引入一個多方委員會(multi-party committee),由這個委員會負責存儲數據副本,並在提供商作惡或終止服務的情況下將數據副本分享給用戶。
但是,將數據存儲在鏈下有一個很大的優勢:更高的可擴展性。採用鏈下存儲的解決方案無需受制於區塊鏈的局限性。因此,相比採用鏈上存儲的解決方案,這類方案更有助於提高交易吞吐量。
最近,StarkWare 提出了一種混合式解決方案,可以讓用戶自由選擇將數據存儲在鏈上還是鏈下。用戶每發起一筆交易都可以選擇一次,因此他們的選擇是動態變化的。這種可擴展性解決方案被稱為 Volition。
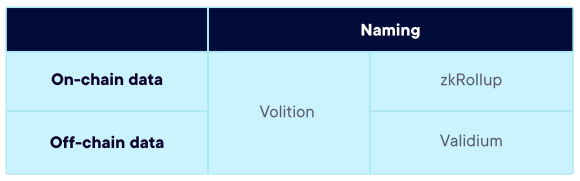
- 來源:https://medium.com/starkware/volition-and-the-emerging-data-availability-spectrum-87e8bfa09bb -
原文鏈接:
https://ethworks.io/ethereum-scaling-report.html
作者: EthWorks
翻譯&校對 :
閔敏& 安比實驗室

















