在傳統金融市場上,每種證券都需要一個買方和賣方市場才能有效地進行交易。如今,股票交易的速度和簡便性被視為理所當然,尤其是在新引入的Robinhood投資模式下。在這個新時代,做市商扮演著舉足輕重的角色,為市場參與者創造了無縫的交易體驗。在過去的一年裡,做市商這個角色以名為自動化做市商(AMMs)的算法代理的形式移植到加密生態系統中。
AMMs執行的功能與傳統做市商相同,促進兩種數字資產之間的交易。然而,在智能合約裡不是由大銀行或交易公司來做市,而是通過算法做市。與傳統的做市商依靠大量資源提供嚴格的買賣價差不同,AMMs重新定義了提供流動性的方式,並應用數學公式來決定資產交易的價格。
1 恆定函數做市商
恆定函數做市商(CFMM)是最流行的AMM系列。當交易者希望將代幣A換成代幣B時,這種AMM會使用恆定函數作為其定價機制。在這種情況下,術語"恆定函數"指的是資產儲備的乘積必須在發生任意交易時都保持不變。
自2017年以來,針對不同使用案例的優化,一些DEX已經把這個恆定函數進行了修改。下面將介紹一些最流行的DEX,並詳細介紹其採用的恆定函數。
2 Uniswap
Uniswap是第一個讓使用恆定函數(來交換兩種資產)變得流行的DEX。它使用了一種被稱為"恆定乘積AMM "的AMM變體,它強制要求兩種資產儲備量的乘積必須始終保持不變。
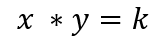
在這個等式中,x和y代表流動性池中兩種資產的單位數量。
舉例說明,假設ETH/DAI池包含100 ETH(x的值)和10,000 DAI(y的值)。在這個例子中,Uniswap將這兩個數量相乘,得到k的值為1,000,000。現在的目標是保持k值恆定,而不考慮對流動性池的交易量。做到這一點的唯一方法是,x和y的數量反向變化。換句話說,當x的數量增加時(交易者將ETH加入池中),y的數量必須減少(交易者將DAI從池中取出)。最終,任何給定交易所的報價都是常量乘積公式和池中代幣比例的函數。
需要注意的是,x和y之間的關係不是線性的。用10個ETH兌換1000個DAI不等於用20個ETH兌換2000個DAI。相反,這種關係是漸近式的。這意味著隨著花費的代幣數量增加,收到的代幣數量會變小。
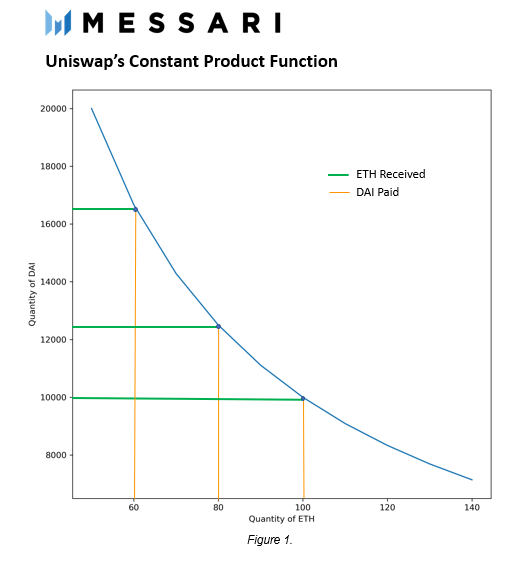
恆定乘積函數的特性對AMMs很有用,因為它確保了當任何一種資產的價格接近無窮大時,總會有流動性。
3 Balancer
Balancer的AMM一般化了Uniswap的恆定乘積功能,創造了一個被稱為"恆定平均AMM"的變體。這個AMM的核心是價值函數,它強制規定資產池中的資產餘額的權重次冪的乘積應始終保持不變。

在這個公式中,t代表池中的資產的種類數,Bt是資產數量,Wt是資產權重。雖然與Uniswap簡單易懂的常量乘積函數相比,數學公式看起來要復雜得多,但其實很容易理解。例如,假設用戶創建了一個Balancer Pool,其中包含三種資產:100 ETH、100 BTC和100,000 DAI,每種資產的權重為33.3%。 Balancer對這些數值進行如下處理:

類似於Uniswap,目標是在保持資產權重不變的情況下,只改變資產餘額,從而保持k不變。在3種資產Balancer Pool的情況下,交易可以發生在三個資產中的任意兩個之間。用戶可以用ETH交換DAI,用ETH交換BTC,或者用DAI交換ETH。通過保持k的值不變,可以在三種資產之間生成一個價值面。
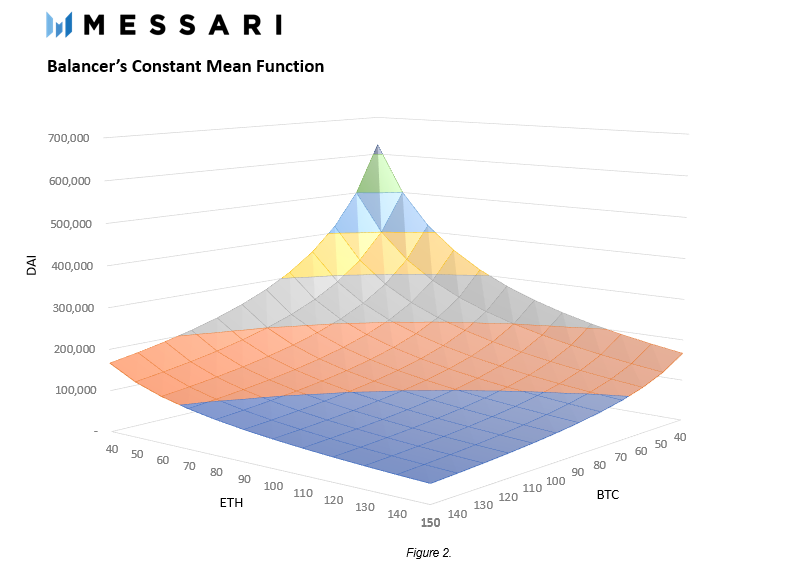
有趣的是,這個曲面與Uniswap的常量乘積函數並沒有太大區別。另一種思考方式是將圖1中的恆積函數,額外增加一個代表池中第三個代幣的軸。通過改變圖2的角度,兩個函數之間的相似性變得更加明顯。
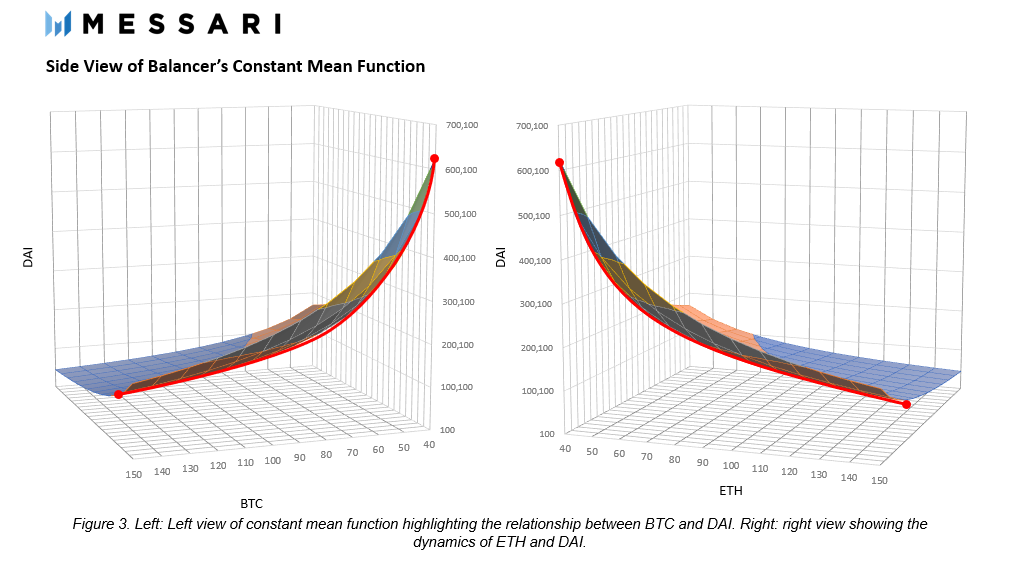
由於Balancer池被設計成有2到8種資產,任意兩個代幣之間的交易價格報價就比較複雜了。池中的每一對代幣都有一個價格,這個價格取決於該特定代幣的餘額B和權重W。從形式上看,交易執行的價格是按照代幣餘額與代幣權重的比值來計算的。

在上面的公式中,代幣A代表被賣出的代幣(進入池子) 而代幣B是被買入的代幣(離開池子)。如果池子的持有者不改變資產儲備,很容易看出價格的變化完全基於交易,因為資產權重必須始終保持不變。這種機制與圖2所示的恆定面相結合,可以保證買入資產的價格上升,而賣出資產的價格下降。在與Uniswap相同的情況下,套利機會保證了Balancer Pools提供的價格與市場其他部分同步變動。
4 Curve
Curve是一個交易所流動性池,預期價格穩定的資產之間可以在該池裡進行高效交易(如穩定幣或封裝的比特幣(wrapped bitcoin))。 Uniswap和Balancer主要是針對波動和價格不穩定的代幣的交易。然而,當處理那些想要互相保持穩定的資產之間的交易時,低價格滑點是最重要的。之前迭代的各種AMMs固有曲率就有問題了,因為交易規模越大,滑點就越大。
解決價格滑點問題的一個方法是,使用常數和函數作為AMM的內部交易機制。當使用兩種資產進行操作時,恆和(constant sum)做市商強制規定資產數量之和必須保持不變,並遵循以下函數:
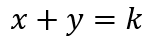
如圖,一個雙資產恆和做市商是一條簡單的直線。
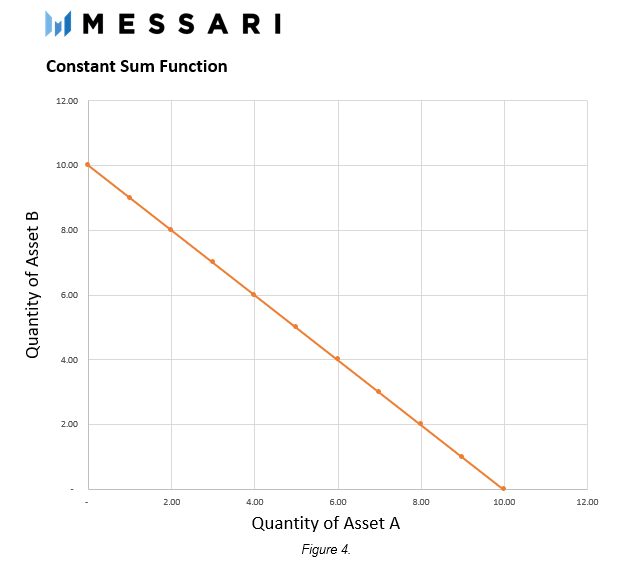
雖然這個函數的簡單性實現了低滑點,但它缺乏恆定產品做市商的關鍵屬性,即當任何一種資產從池子中流出時,池子總還會有流動性,而另一種資產的數量趨於無窮大。
為了解決這些問題,Curve通過結合恆定總和和恆定乘積函數創造了一種混合AMM:在曲線的平衡點附近創建一條相對平坦的曲線,類似於恆定總和函數,以保持價格相對穩定,同時使兩端更加傾斜,類似於恆定乘積函數,因此在曲線的每個點都有流動性。在雙資產的情況下(x和y),最終的結果是下面的複雜函數。
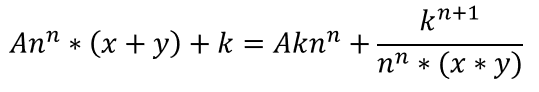
除了複雜的數學之外,請注意兩個常數函數是如何嵌入方程中的。左邊是常數和,右手邊是常數積。此外,公式中還包含了一些其他的項來達到預期的目的。在公式中,n代表資產數量(在本例中n=2),A是一個"放大係數"參數,它決定了函數與常積函數的相似程度。 A的值越低,Curve的函數就越接近Uniswap的函數。
就像之前的CFMMs一樣,我們的目標是在x和y之間發生交換時保持k的值不變。繪製該函數會像這樣:
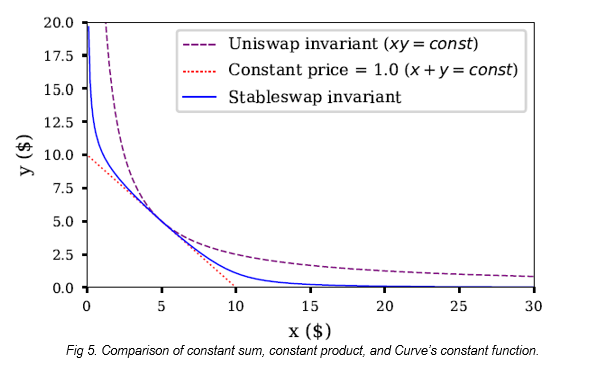
來源:Curve白皮書
從圖5中可以看出,Curve的函數在中間表現為恆定加和函數,但隨著x和y的值的變大,則變為恆定乘積函數。這種形狀使曲線中間段的價格保持穩定,同時又能在兩端提供流動性。
結論
在過去的幾年裡,AMMs通過以去中心化的、全球可訪問的和非託管的方式匯聚和提供流動性,它已經成為DeFi的重要組成部分。具體而言,Uniswap、Balancer和Curve等CFMMs獲得了巨大的增長和應用,交易量超過數十億美元。
自2017年以來,這些去中心化的交易所已經開發了恆定函數的各種變體,以解決特定的交易所問題。隨著該領域繼續擴大,涵蓋各種資產,為使交易更高效,交易所必須對底層功能進行大量思考。雖然這項技術仍處於早期階段,但它已經帶出了新的研究領域,更多的AMM設計將會出現,最終為所有DeFi用戶提供更好的流動性。

















