本文作者是Mechanism Capital 研究員Benjamin Simon,本文通過AMPL和Basis實例分析了算法穩定幣面臨的問題以及算法穩定幣的優點。作者認為算法穩定幣是一種有吸引力的貨幣實驗,在此早期階段關閉算法穩定幣將是愚蠢的,但其風險也不能被忽視。
2014年,兩篇學術論文正式發布:一篇是由費迪南多·阿梅特拉諾(Ferdinando Ametrano)編寫的《Hayek Money:加密貨幣價格穩定解決方案》,另一篇是由羅伯特·薩姆斯(Robert Sams)編寫的》關於加密貨幣穩定性的注意事項:鑄幣稅股份》。
借鑒弗里德里希·哈耶克(Friedrich Hayek)對黃金標準的批評,阿梅特拉諾(Ametrano)認為,由於通縮性,比特幣無法充分執行我們要求的貨幣單位制。取而代之的是,他提出了一種基於規則的,供應彈性的加密貨幣,可以根據需求進行``調整""(即改變所有代幣持有者在貨幣供應中佔的比例)。
薩姆斯(Sams)在《鑄幣稅股份》文中提出了一種具有相似理由的相似模型,但有一個重要的轉折。 Sams的系統取代了在所有錢包中按比例分配貨幣供應量的“基礎”貨幣,而是由兩個代幣組成:這種供應彈性的貨幣本身和在網絡中的投資“份額”。後者資產的所有者(Sams稱其為“鑄幣稅股份”)是正向供應增加帶來的通貨膨脹收益的唯一接受者,而當貨幣需求下降且網絡收縮時則是債務負擔的唯一承擔者。
精明的加密貨幣觀察家將認識到Ametrano的《Hayek Money》和Sams的《鑄幣稅股份》不再是學術抽象。 《Hayek Money》幾乎就是現在的Ampleforth,後者於2019年推出,並於2020年7月猛增至市值超過10億美元。最近,薩姆斯(Sams)的《鑄幣稅份額》模型在不同程度上為Basis,Empty Set Dollar,Basis Cash和Frax等算法穩定幣奠定了基礎。
現在擺在我們面前的問題與六年前Ametrano和Sams論文的讀者面臨問題沒有什麼不同:算法穩定幣能否真正實現長期生存能力?算法穩定幣會一直受到極端的擴張和收縮週期影響嗎?哪種算法的穩定幣更引人注目:一個簡單的基礎模型或一個多代幣的“鑄幣稅”系統(或完全其他的東西)?
在所有這些問題上,都仍未解決,可能需要一段時間才能達成廣泛共識。儘管如此,本文還是試圖從第一性原理的推理以及最近幾個月的一些經驗數據中探究其中一些基本問題。
1
穩定幣背景
算法穩定幣本身就是一個世界,但是在深入研究之前,值得退後一步,調查一下更廣泛的穩定幣前景。 (已經熟悉穩定幣的讀者可以略過或跳過本節。)
由於比特幣的機構採用滾雪球般地向前發展,DeFi夏季熱潮以及以太坊即將進行的網絡升級,穩定幣近來讓人驚訝不已,總市值已超過250億美元。這種拋物線式的增長吸引了密碼學界以外的強大個體的眼球,其中包括最近一批美國立法者。
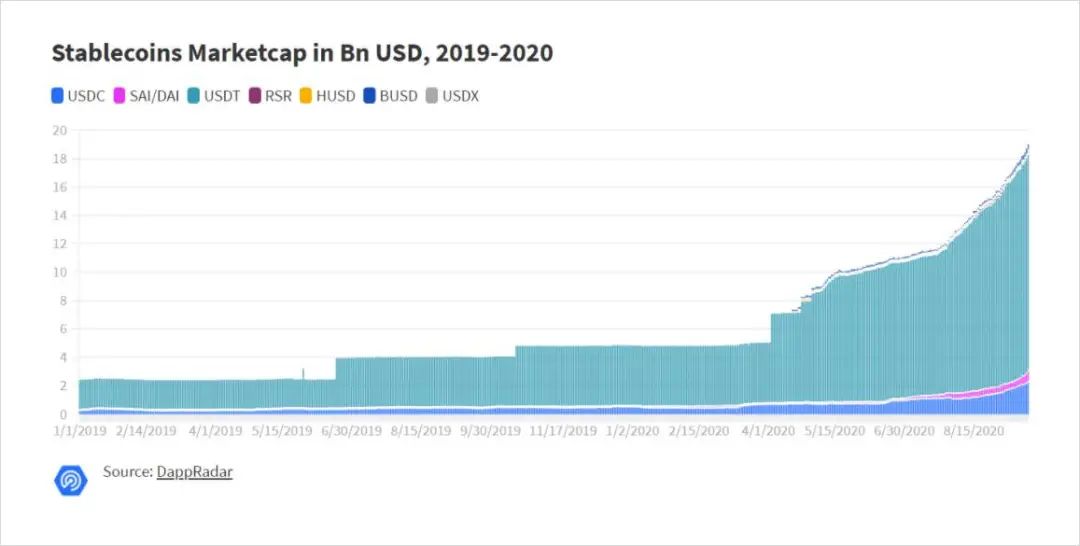
USDT仍然是主要的穩定幣,但它遠非唯一的穩定幣。廣義上講,我們可以將穩定幣分為三類:美元抵押型,多資產池過度抵押型和算法型(1)。我們在本文中的重點是最後一個類別。但是,重要的是要注意穩定幣在其他類別中的優缺點,因為理解這些折衷方案將使我們能夠提高算法穩定幣的價值主張。
第一類穩定幣(即USDT和USDC,但也包括基於交易所的代幣(平台幣),如BUSD)由中心化管理的,由美元提供支撐並且1:1可贖回。這些穩定幣具有一種受到保證的掛鉤和資本高效的優點(即沒有過度抵押),但是它們的中心化性質意味著用戶可以被列入黑名單,而掛鉤本身取決於中央實體的可信賴行為。
第二類是多資產抵押穩定幣,包括MakerDAO的DAI和Synthetix的sUSD。這兩種穩定幣都被加密資產超額抵押,並且都依靠價格預言機來維持與美元掛鉤。與USDT和USDC等中心化代幣不同,它們可以無需許可地被鑄造(DAI),值得注意的是,可以將USDC等經過許可的中心化資產用作抵押品。此外,這些穩定幣的超額抵押性質意味著它們非常資本密集,並且加密資產的高度動盪,高度相關的性質使這些穩定幣在過去容易受到加密震蕩的衝擊。
所有這些使我們進入了算法穩定幣。算法穩定幣是一種確定性地(即使用算法)調整其供應量的代幣,以使代幣的價格朝價格目標(2)的方向移動。在最基本的水平上,算法穩定幣在高於目標價格時會擴大其供應,而在低於目標價格時則會收縮。
與其他兩種類型的穩定幣不同,算法穩定幣既不能以美元一對一地贖回,也沒有目前由加密資產抵押支持(3)。最後,也許也是最重要的一點是,算法穩定幣通常具有很高的反身性(reflexive):需求在很大程度上是由市場情緒和動力驅動的,這一點受到很多爭論。這些需求方的力量被轉移到代幣供應中,進而在最終成為暴力反饋迴路的方向上產生進一步的方向動量。
每種穩定幣模型都有其權衡。很少關注中心化的投資者將不會對USDT和USDC有任何問題。其他人會發現,資本效率低下的過度抵押是值得付出的代價,以獲得一種堅定錨定的無需許可且去中心化的貨幣。但是,對於那些對這兩個選項都不滿意的人,算法穩定幣是一個誘人的選擇。
2
算法穩定性的反身性與悖論
為了使算法穩定幣長期可行,它們必須實現穩定性。對於許多算法穩定幣而言,由於其固有的反身性,因此特別難以實現此任務。算法上的供應變化旨在是反週期的;擴大供應量應降低價格,反之亦然。然而,實際上,供應變化通常會自發地放大方向動量(4),特別是對於不遵循“鑄幣稅股份”模型的算法模型,即通過將穩定幣代幣與價值產生代幣和債務融資代幣分離開來。
對於非算法穩定幣,網絡引導不涉及博弈論的協調。每個穩定幣(至少在理論上來說)可兌換等值的美元或其他形式的抵押品(5)。相比之下,算法穩定幣的成功價格穩定性完全無法保證,因為它完全由集體市場心理決定。 Haseeb Qureshi恰當地指出了這一點:“這些計劃利用了一個關鍵見解:穩定幣最終是一個Schelling點。如果足夠多的人相信該系統能夠生存,那麼這種信念就會導致確保其生存的良性循環。”
的確,如果我們更加仔細地考慮算法穩定幣要實現長期穩定將需要什麼,我們會發現一個明顯的悖論。為了實現價格穩定,算法穩定幣必須擴展到足夠大的市值,以使買賣訂單不會引起價格波動。但是,純算法穩定幣增長到足夠大的網絡規模的唯一方法是通過投機和反身性,而高反身性增長的問題在於它是不可持續的,並且收縮通常也是反身性的。因此,自相矛盾:穩定幣的網絡價值越大,它對大價格衝擊的適應力就越大。然而,只有高度反身的算法穩定幣(易於出現極端的擴張/收縮週期的那些幣)才有可能首先達到大型網絡估值。
反身性也有類似的悖論。為了使它對越來越多的人和組織可行,它必須越來越具有流動性,穩定性和接受性。多年來,比特幣的這些特徵不斷增長,使其被最初的暗網參與者,後來的富裕技術人員以及最近的傳統金融機構所接受。在這一點上,比特幣已經在反身周期的深度中獲得了抵抗力,這是算法穩定幣也需要遵循的路徑。
3
Ampleforth:一個簡單但有缺陷的算法穩定幣
現在讓我們從抽象理論轉向算法穩定幣的現實世界,首先從當今存在的最大但最簡單的協議開始:Ampleforth。
如前所述,Ampleforth(AMPL)與Ferdinando Ametrano提出的《Hayek Money》概念幾乎相同。 AMPL的供應根據每個AMPL的每日時間加權平均價格(TWAP)根據確定性規則進行擴展和收縮:低於價格目標範圍(即,低於0.96美元),供應收縮;高於價格目標範圍(即,高於1.06美元) ,供應增加。至關重要的是,每個錢包都按比例“參與”了每次供應變化。如果在rebase之前愛麗絲持有1,000個AMPL,而供應量增加了10%,那麼愛麗絲現在將持有1,100;如果Bob擁有1個AMPL,那麼他現在擁有1.1個AMPL。
網絡範圍內的“rebase”是將Ampleforth的算法模型與其他協議採用的鑄幣稅份額模型的區分之處。儘管Ampleforth白皮書沒有提供與多代幣方法相對的單代幣rebasing的基本原理,但該設計決策似乎有兩個主要依據。
首先是簡單性。無論它在實踐中如何運作,Ampleforth的單代幣模型都具有其他算法穩定幣無法比擬的優雅簡潔性。其次,Ampleforth的單代幣設計聲稱是最公平的算法穩定幣模型。與法定貨幣政策行動形成鮮明對比的是,法定貨幣政策行動使那些“最接近”貨幣來源的個人受益最大(“坎蒂隆效應”),Ampleforth的設計使所有代幣持有人在每次重新設定基調後都能保持相同的網絡份額。阿美特拉諾(Ametrano)在2014年的論文中指出了這一點,他詳細介紹了貨幣政策行動的“嚴重不公平”,並將其與《Hayek Money》的相對公平性進行了對比。
這就是Ampleforth模型的推定理由,該模型已被其他rebasing代幣(如BASED和YAM)複製。但是,在探討該模型的缺陷之前,我們可能首先要查看可供我們使用的有關Ampleforth表現的一年半數據。自從2019年中期開始(僅超過500天)以來,Ampleforth的每日資產調整中有四分之三是正數或負數,換句話說,自啟動以來,AMPL的TWAP已超出目標範圍的75%以上。可以肯定的是,該協議仍處於起步階段,因此僅憑這些理由將其否定還為時過早。儘管如此,我們很快將研究經過修改的“鑄幣稅”穩定幣Empty Set Dollar,在其誕生的頭幾個月中,如何保持比Ampleforth穩定兩倍以上的穩定性。

Ampleforth的捍衛者經常擺脫缺乏穩定性的想法;他們中的許多人甚至會討厭“算法穩定幣”的標籤。他們的論點是,使Ampleforth成為投資組合多元化的“不相關的儲備資產”就足夠了。但是,這種說法值得懷疑。例如,根據隨機數生成器每天rebase的一種加密貨幣。像Ampleforth一樣,該代幣將具有“明顯的波動足跡”,但僅憑這個原因,它肯定不會有價值。 Ampleforth的價值主張取決於其趨於均衡的趨勢,這一品質理論上可使AMPL成為價格標價的貨幣。
但是會嗎?想像一下,如果Ampleforth擺脫了至今的“粘性”性質,並將價格波動完全轉移到了供應波動中,從而每個AMPL的價格將基本保持穩定。這個“成熟的” Ampleforth是否真的是交易基礎貨幣的理想選擇?
在這裡,我們討論了問題的癥結所在以及Ampleforth設計的中心缺陷。即使AMPL的價格達到1美元,個人持有的AMPL的購買力也會在達到1美元的過程中發生變化。早在2014年,羅伯特·薩姆斯(Robert Sams)就Ametrano的《Hayek Money》闡明了這一確切問題:
價格穩定不僅關係到穩定計價單位,還關係到穩定貨幣的價值存儲。 《Hayek Money》旨在解決前者,而不是後者。它只是將固定的錢包餘額與波動的代幣價格進行交易,將固定的代幣價格與波動的錢包餘額進行交易。最終結果是,《Hayek Money》錢包的購買力與比特幣錢包餘額一樣不穩定。
最終,Ampleforth的簡單性(其簡單的單代幣rebasing模型)是一個錯誤,而不是功能。 AMPL代幣是一種投機工具,當需求高時會獎勵持有人通貨膨脹,而當需求低時則迫使持有人成為債務融資人。因此,很難看到AMPL如何既可以達到這一投機目的,又可以實現穩定性,這是穩定幣的必要先決條件。
4
多代幣“鑄幣稅”替代選擇
羅伯特·薩姆斯(Robert Sams)的《鑄幣稅股份》願景從未成為現實,但是最近出現了一種新型的算法穩定幣項目,該項目具有許多核心要素。
僅僅誕生一周多的時間,Basis Cash是對複興Basis的公開嘗試,Basis Cash是一個算法穩定幣項目,在2018年籌集了超過1億美元的資金,儘管倍受讚譽,但從未最終啟動。與Basis一樣,Basis Cash是一個多代幣協議,由三個代幣組成:BAC(算法穩定幣),Basis Cash Shares(網絡擴展時其持有人可以要求BAC通脹)和Basis Cash Bonds(可以購買)當網絡處於收縮狀態時可以打折,並且可以在網絡退出通縮階段時兌換為BAC。 Basis Cash仍處於開發的早期階段,並且遇到了一些早期開發障礙。該協議尚未進行成功的供應變更。
但是,自9月份以來,又有另一個鑄幣稅股份式協議“Empty Set Dollar(ESD)”生效,並且已經經歷了多個供應擴展和收縮週期。實際上,到目前為止,ESD已經歷達到200多次供應“時期”(每八小時一次),其中60%發生在當ESD的TWAP在$ 0.95 
乍一看,ESD的機制設計似乎是Basis和Ampleforth的混合體。像Basis(和Basis Cash)一樣,ESD利用債券(“優惠券”)來資助協議債務,債務必須通過銷毀ESD來購買(因此通過合約供應),並且可以在協議擴展後贖回為ESD。但是,與Basis不同,ESD沒有第三個代幣,該代幣在網絡在還清債務後(即在贖回票息後)擴展時要求通貨膨脹獎勵。代替這第三個代幣,ESD持有者可以在ESD DAO中“綁定”(即參股)其ESD,以按比例分配每次代幣擴張的份額,類似於Ampleforth的rebase。
至關重要的是,與DAO解除綁定的ESD需要一個“暫存”期,其中ESD代幣被臨時“暫存” 15個週期(5天),既不能由其所有者交易也不能獲得通貨膨脹獎勵。因此,ESD的分階段模型的功能類似於Basis Cash Shares,因為將ESD綁定到DAO併購買Basis Cash Shares都預先假設了風險(ESD的流動性風險;BAS的價格風險)具有未來的通貨膨脹獎勵的潛力。確實,儘管ESD使用兩代幣模型(ESD和優惠券)代替了Basis Cash的三代幣模型,但ESD暫存期的最終結果是ESD變成了事實上的三代幣系統,並以綁定的ESD作為模擬Basis Cash Shares。
5
對比單代幣和多代幣算法穩定幣模型
顯然,與Ampleforth的單代幣rebase模型相比,多代幣rebase設計包含了更多變化的部分。然而,這種增加的複雜性對於為其提供的潛在穩定性來說是一個很小的代價。
簡而言之,ESD和Basis Cash採用的設計的結果是,包含了系統固有的反身性,而係統的“穩定幣”部分則(在某種程度上)與市場動態隔離(10)。具有風險偏好的投機者可以在供應收縮期間引導協議,以換取將來從擴展中受益。但是,僅在理論上,僅希望擁有具有穩定購買力的穩定幣的用戶就可以持有BAC或ESD,而無需購買債券,息票,股票或將其代幣綁定到DAO。這種無rebasing的性質具有與其他DeFi原語可組合性的額外好處。與AMPL不同,BAC和(無綁定)ESD可以用作抵押或借出,而不必考慮網絡範圍內持續不斷的供應變化的複雜動態。
Ampleforth創始人兼首席執行官Evan Kuo批評像Basis Cash這樣的算法穩定幣項目,因為它們“依靠債務市場(即債券)來調節供應。Kuo勸告人們不要使用這些“殭屍思想”,因為這些算法穩定幣是有缺陷的,因為像傳統市場一樣,它們“將始終依靠最後的放款人(即紓困)”。
但是,Kuo的論點是有疑問的,因為它假設的條件是缺乏任何理論依據,依賴債務市場(“紓困”)本質上是危險的。實際上,由於道德風險,債務融資在傳統市場中是有問題的。 “太大而不能倒閉”的企業實體可以通過將紓困成本社會化來承擔未受到懲罰的風險。像ESD和Basis Cash這樣的算法穩定幣不具有房利美和房地美在2008年金融危機期間享有的奢侈支持。對於這些協議,系統之外沒有最後的貸款人可以將救助成本轉移到該貸方。 ESD或Basis Cash完全有可能陷入債務螺旋式增長,在這種螺旋式中,債務堆積而沒有金融家的意願,協議就崩潰了。
實際上,Ampleforth還要求債務融資,以避免死亡螺旋上升。所不同的是,這種債務融資隱藏在大眾目光之下,因為它分佈在所有網絡參與者中。與ESD和Basis Cash不同,如果不同時充當協議的投資者,就無法加入Ampleforth系統。在網絡處於收縮狀態時持有AMPL類似於承擔該網絡的債務(使用Maple Leaf Capital的措辭為“充當中央銀行”),因為AMPL持有者會在每次負供應基礎上損失代幣。
從第一性原理推論和經驗數據來看,我們可以得出結論,與“單代幣rebasing”替代方案相比,這種多代幣且受“鑄幣稅股份”啟發的模型具有明顯更高的內置穩定性。的確,費迪南多·阿梅特拉諾(Ferdinando Ametrano)最近從2014年開始更新了他對《Hayek Money》的“第一個簡單化實現”,鑑於上述問題,他現在讚成基於多代幣,基於鑄幣稅的模型。
然而,即使多代幣算法穩定幣優於其單代幣同行,也無法保證這些算法穩定幣中的任何一種都能長期持續發展。確實,算法穩定幣的底層機制設計排除了任何此類保證,因為如上所述,算法穩定幣的穩定性最終是基於博弈論協調的反身性現象。即使對於像ESD和Basis Cash這樣的協議,它們將交易,穩定購買力代幣與價值應計和債務融資代幣分離開來,只要有投資者願意,穩定代幣就將保持穩定。在需求下降時引導網絡。當不再有足夠的投機者認為網絡具有彈性時,網絡將不再具有彈性。
6
部分儲備穩定幣:算法穩定幣的新時代?
純算法穩定幣所具有的投機性是不可避免的。但是,最近出現了一些雛形協議,試圖通過利用部分資產抵押(“部分儲備”)來控制算法穩定幣的反身性。
這裡的見解很簡單。 Haseeb Qureshi在他的觀察中是正確的,“從根本上講,您可以說支持鑄幣稅股份的"抵押"是系統未來增長中的股份。” 那麼為什麼不以實際抵押品補充這種投機性“抵押品”,以使系統更強大呢?
ESD v2和Frax正是這樣做的。 ESD v2仍處於研究和討論階段,此後最終將由治理部門投票表決。如果實施,這個升級將對當前的ESD協議進行幾項實質性更改。其中最主要的是引入“儲備金要求”。
在新系統下,ESD協議的目標是20%至30%的儲備金率,最初以USDC計價。這些儲備的部分資金來自協議本身,該協議會在ESD高於某個目標價格時在公開市場上出售ESD,並且也希望由想要與DAO解除綁定的ESD持有者(他們必須向儲備金進行存款)。然後,通過自動購買ESD直到達到最低儲備要求,這些USDC儲備可用於在收縮期間穩定協議。
尚未推出的Frax是創建部分抵押算法穩定幣的更為優雅的嘗試。與基礎現金一樣,Frax包含三個代幣:FRAX(穩定幣),Frax股票(管理和價值應計代幣)和Frax債券(債務融資代幣)。但是,與到目前為止討論的所有其他算法穩定幣不同,FRAX可以始終以1美元的價格鑄造和贖回,這意味著套利者將在穩定代幣價格方面發揮積極作用。
這種鑄造/兌換機制是Frax網絡的核心,因為它利用了動態的分數儲備系統。要鑄造一個FRAX,用戶必須存入一定數量的Frax股票(FXS)和其他價值一美元的抵押品(USDC或USDT)組合。 FXS與其他抵押品的比例由對FRAX的需求動態確定(隨著需求的增加,FXS與其他抵押品的比例會增加)。鎖定FXS來鑄造FRAX將對FXS供應產生通縮效應,因此,隨著需要更多FXS鑄造FRAX,對FXS的需求自然會隨著供應下降而增加。相反,正如Frax的文檔所指出的,在收縮期間,“該協議對系統進行了抵押,以使FRAX的贖回者從系統中獲得更多的FXS和更少的抵押品。這增加了系統中抵押品佔FRAX供應比例的比例,隨著FRAX的支持增加,市場對FRAX的信心也增強了。”
有效地,動態抵押充當穩定的反週期機制,使Frax協議可以在需要時鈍化極度反身性的有害影響。但是,如果市場選擇的話,它還允許該協議在將來變得完全無抵押成為可能。從這個意義上講,Frax的動態抵押機制是“不可知論的”。
Frax和ESD v2均未啟用,因此在實踐中能否成功還有待觀察。但是至少從理論上講,這些混合的,部分儲備的協議是將反身性與穩定性結合起來的有前途的嘗試,同時仍然比DAI和sUSD等過度抵押的替代方案具有更高的資本效率。
結論思想
算法穩定幣是一種具有吸引力的是貨幣實驗。儘管查理·芒格(Charlie Munger)的格言始終如一:“告訴我動機,我告訴你結果”,但這些協議具有博弈論上的複雜性,僅憑先驗推理就很難完全把握住。此外,如果過去的加密貨幣市場週期可以作為指引,我們應該為這些動態做好準備,以掩蓋理性預期的方式發揮作用。
然而,在此早期階段關閉算法穩定幣將是愚蠢的。忘記賭注到底有多高也是錯誤的。哈耶克(Hayek)在1976年的《貨幣貶值》中寫道:“我相信我們可以做得比黃金更好。政府不能做得更好。自由企業,即毫無疑問會從競爭過程中產生的提供優質資金的機構。”儘管算法穩定幣仍處於混亂狀態,但它們最終可能成為哈耶克關於蓬勃發展的貨幣市場的願景的藍圖,並為之奠定基礎。
披露:作者可能持有本文提到的代幣。















