
作者:Leo Liu, Guangwu Xie
翻譯:Vanessa Cao
校對:Leo Liu, Guangwu Xie
排版:Jane Hu
感謝:Fangyuan Zhao, Showen Peng, DW, Lianxuan Li, Dave White, Dan Robinson, Vanessa Cao, Jane Hu
本文總共分為中篇闡述自動做市商算法、現狀及未來迭代的思考,本文為下篇。
目錄
16. 為Curve V2 設計更好的動態權重
17. 當價格函數為非解析時應用價格範圍
18. Clipper:針對小額交易優化的AMM 算法
19. TWAMM:針對大額長期訂單優化的AMM 算法
20. TWAMM 在恆定乘積做市商(CPMM) 和對數市場評分規則(LMSR) 上的應用
21. TWAMM 在YieldSpace 等與時間相關的AMM 上的應用
22. 結論和未來工作
為Curve V2 設計更好的動態權重:
γ值
在
Curve V2 中,有一個常數稱為
γ
。
如果我們也讓它動態化,會發生什麼?
例如,我們可以使它成為
K0
的函數。
最簡單的情況是使其等於
K0
。
這裡的動機是讓函數在接近平衡點時表現得更像StableSwap,當函數遠離平衡點時,使其更像CPMM。
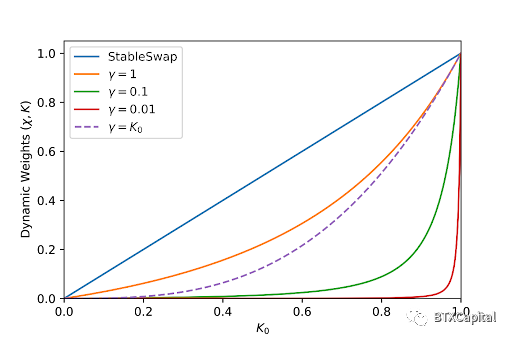
紫色虛線曲線位於StableSwap 和小γ 值曲線之間,應該為我們提供StableSwap 和Curve V2 之間的做市商函數。然而,當我們繪製做市商函數時,它的圖像跟StableSwap 很相似:
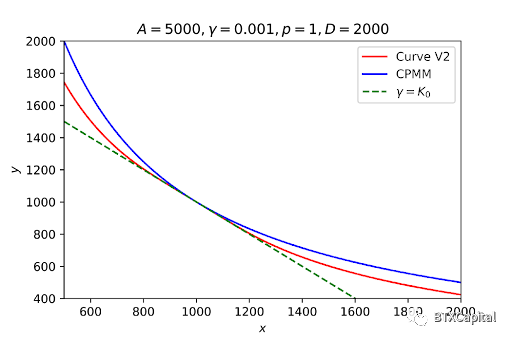
這個問題有兩種解決方案:1. 使A 更小2. 選擇K0 的較高冪數來表示γ。兩者似乎都是可行的, 然而1. 破壞了A 作為一個大數的目的:使做市商函數與價格錨定。我們進行的進一步測試似乎表明,更改A 不會對函數行為產生影響(更改A 後做市商函數仍然看起來像StableSwap)。
第二種解決方案會使gas費用更高。 K0 的更高次冪數對應於我們需要求解的更高階多項式方程。事實上,Curve V2 選擇動態權重K 的特定形式的原因是為了模擬大指數K0 的函數行為,同時不使多項式的階數更高。
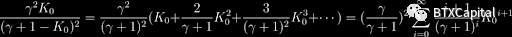
有趣的問題是:我們能否找到一個更好的動態權重來簡化我們需要求解的方程,同時保持與Curve V2 相同或更好的功能?在設計這樣的動態權重時,我們還必須記住,我們需要在小滑點和做市商函數對預知市場未來的大訂單做出反應的能力之間保持平衡。顯然,只有價格錨定的StableSwap 在這方面是行不通的,因為如果錨定價格與市場價格不同,幾乎所有的代幣都會被買斷。只有在保持這種平衡的情況下,價格重錨才可行。
當價格函數為非解析時應用價格範圍:
我們可以將價格範圍概念應用於Curve V2。由於沒有關於池中代幣數量的價格解析表達式,我們需要擬合價格和代幣數量之間的關係。應用於做市商函數的偏移量由價格範圍決定。編寫這樣的程序可以使資本效率更高。
Clipper:針對小額交易優化的AMM 算法:
Clipper¹³
使用最適合小額交易需求的AMM 算法。它將恆定乘積做市商(CPMM) 和恆定總和做市商(CSMM) 概括為兩個極端情況(k = 1 和k = 0)。
Clipper¹³:New Invariants for Automated Market Makinghttps://github.com/shipyard-software/market-making-whitepaper/blob/main/paper.pdf

當只有兩種類型的代幣(X 和Y)時,不變量可以簡化為更簡單的形式,其中x0 和y0 是初始流動性提供者設置的代幣數量。以下是流動性池在不同k 值下的行為。 x 和y 軸由x0 和y0 歸一化。
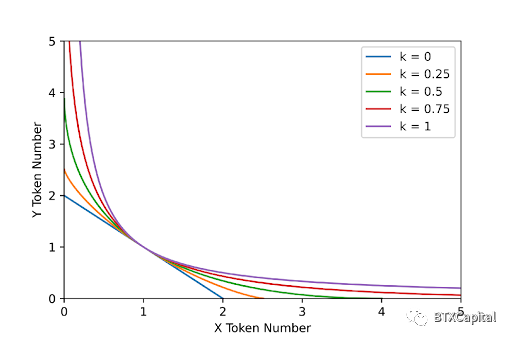
較小的k 值對應於(1, 1) 附近的較低滑點(函數不太凸)。當k 介於0 和1 之間時,不變函數可以與x 和y 軸相交。這意味著池中的代幣可能會售罄。該交叉點的價格為零,這意味著該價格在轉折點之前優於CPMM 價格。過了轉折點後,CPMM的價格比較好。這可以在下圖中說明:
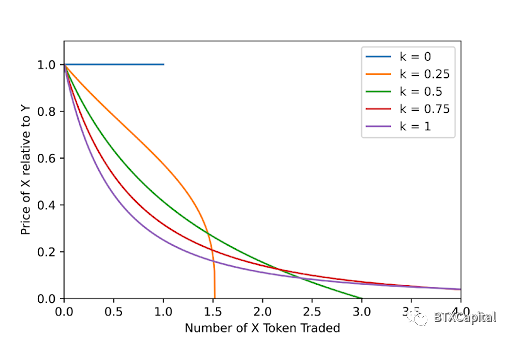
再次對x 軸進行歸一化。隨著我們遠離初始點(1, 1),X 代幣相對於Y 的價格下降。我們可以精確計算交點發生的位置:

優點:
通過引入k,Clipper 在交易量較小時實現了更低的滑點(更好的價格)。 Clipper 白皮書中的以下圖表進一步證明了這一點。
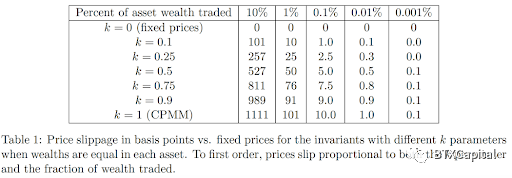
From Clipper whitepaper
缺點:
當交易量超過一定門檻時,價格會明顯低於CPMM。
為了保證更好的價格,算法必須不斷地價格重錨(改變x0 和y0)以保持當前池儲備接近(1, 1) 點。它可以使用與Curve 相同的機制。該算法通過遵循其跟踪市場價格的內部價格預言機進行價格重錨。本質上,這等價於求解下面的公式,但這次x, y 是已知的。 P 由價格預言機給出。最後求解x0 的這個方程給了我們新的平衡點。
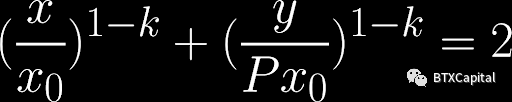
這確保我們始終以較小的滑點接近市場價格進行交易。目前我們還沒有調查Clipper 是否實現了這一點,因為這在Clipper 白皮書中沒有解釋。需要進一步查看其源代碼。
價格範圍概念也可以應用於Clipper:

TWAMM:針對大額長期訂單優化的AMM 算法:
在上面討論的所有AMM 中,我們一次只能在一個方向上進行交易。如果我告訴您最近出現了一種允許同時進行雙向交易的算法呢?
TWAMM¹⁴
(注:時間加權自動做市商,發音為“tee-wham”)算法將一段時間內的長期訂單轉換為無限小的虛擬訂單的積分。訂單可以兩邊同時進行。此外,在同一時間範圍內、同一交易方向執行的訂單會匯集在一起以簡化計算。因此,一段時間內的長期訂單以等於該時期時間加權市場價格的價格執行。
TWAMM¹⁴https://www.paradigm.xyz/2021/07/twamm/
截至目前,只對於兩種類型的AMM,CPMM 和LMSR(注:對數市場評分規則)存在解析形式的TWAMM 解。
讓我們考慮一般情況,在一段時間內,代幣X 的總銷售額為xin,Y 的總銷售額為yin。 X 的賣出率為f(t),Y 的賣出率為
g(t)
。從時間
t
到
t
+
dt
代幣X 數量的淨變化可以計算為代幣X 的銷售數量減去在此期間購買的代幣X 數量,匯率為
dy/dx
。由於在此期間代幣Y 的銷售量無限小,因此可以使用現貨價格作為實際匯率。

因此,我們得到一個非線性一階微分方程。取決於dy/dx、
f(t)
和
g(t)
的形式,方程可能有也可能沒有解析解。
TWAMM 在恆定乘積做市商(CPMM) 和對數市場評分規則(LMSR) 上的應用:
當應用於CPMM 時,方程可以被積分,如果f(t)/g(t) 是一個常數,這意味著代幣X 和Y 的銷售策略是相同的。我們可以進一步簡化表達式:

存在這個積分的解析表達式。利用雙曲函數的性質,我們可以得到一個漂亮的最終解(交易後池中的代幣X數),它只取決於池的原始位置(x0,y0)和
xin,yin
。由於CPMM 的做市商函數關於
x
和
y
完全對稱,因此也可以通過在xend 的最終表達式中交換
xin
和
yin、x0
和
y0
的位置來表示最終的代幣Y 數。代幣X數和代幣Y數的乘積正如預期的那樣等於k。
這種源自CPMM的微分方程形式,實際上有一個數學名稱叫做“Riccati方程”。 Riccati 方程的一般形式如下:
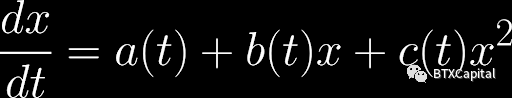
Riccati 方程沒有一般的解析解。但是,存在可以求解Riccati 方程的特殊情況。有一篇
論文¹⁵
討論了這些案例。如果Riccati 方程的係數滿足這個條件:
論文¹⁵:Analytical solutions of the Riccati equation with coefficients satisfying integral or differential conditions with arbitrary functionshttps://arxiv.org/abs/1311.1150

則Riccati 方程可以轉化為Bernoulli 型方程。 Bernoulli型方程可以很容易地求解。這應該給我們與以前相同的結果。從上面我們可以看出,滿足這個條件與保持f(t)/g(t) 恆定相同,這是我們在第一種求解微分方程的方法中假設的。
當
f(t)/g(t)
不是常數時,我們可以選擇什麼形式的f(t) 和
g(t)
使微分方程具有解析解仍然是一個懸而未決的問題。找到這樣的解決方案會給我們更多的選擇(代幣X 和Y 的銷售策略不必相同)。
現在讓我們將TWAMM 應用到LMSR:

同樣,我們假設銷售策略是相同的。然後可以對微分方程進行積分。我們可以進一步簡化最終的代幣X 和Y 數量表達式為:
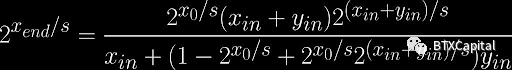
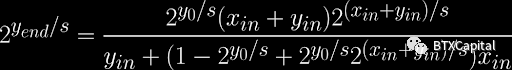
同樣,當銷售策略不同時,也不能保證微分方程具有解析解。
一旦我們獲得了xend 和
yend
,我們就可以計算出每方將收到多少代幣X 和代幣Y:
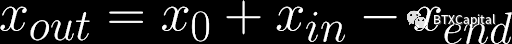
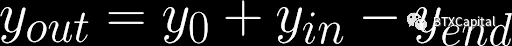
由於在此期間,同一交易方向的所有訂單都匯集在一起。每個個體交易者將根據他對xin 和
yin
的貢獻比例獲得他應得的代幣份額。
優點:
TWAMM 通過允許交易對手同時對這些大訂單進行交易,從而使大訂單的價格滑點更小。在最理想的情況下(
xin/yin
=
x0/y0
),可以實現零滑點交易。在這種情況下,
xend
=
x0
,
yend
=
y0
,TWAMM 可以理解為充當了訂單簿,在不提供流動性的情況下在雙方之間交換代幣。長期訂單被分解成無限小的訂單,這些訂單在區塊之間虛擬執行。由於這種性質,它不太容易受到三明治攻擊,因為攻擊者必須在塊的末尾放置一個命令,並在下一個塊的開頭放置另一個命令。
缺點:
如果我們允許訂單在任何時候到期,gas 費用可能會非常高。這是因為我們必須多次計算積分結果(在論文中他們稱之為“懶惰計算”)。在最壞的情況下,我們必須計算每個塊的結果。
因此,在實踐中我們必須讓訂單在某些區塊到期以簡化計算。
此外,TWAMM 使用的流動性池必須與現有的流動性池不同,
因為沒有虛擬訂單和懶惰計算的概念。普通交易者在與TWAMM 交互時不想支付懶惰計算產生的額外gas 費用(只要有人與之交互,流動性池就會更新)。
TWAMM 在YieldSpace 等與時間相關的AMM 上的應用:
我們還可以將TWAMM 應用於與時間相關的AMM,例如
YieldSpace¹⁶:
YieldSpace¹⁶:An Automated Liquidity Provider for Fixed Yield Tokenshttps://yield.is/YieldSpace.pdf
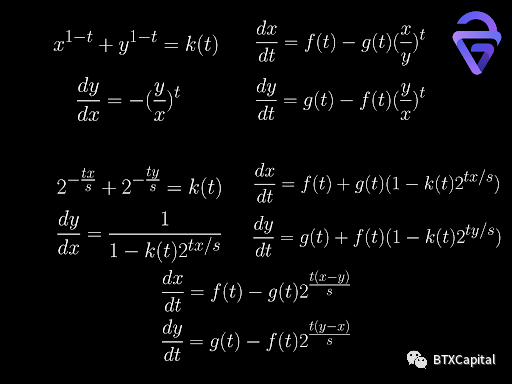
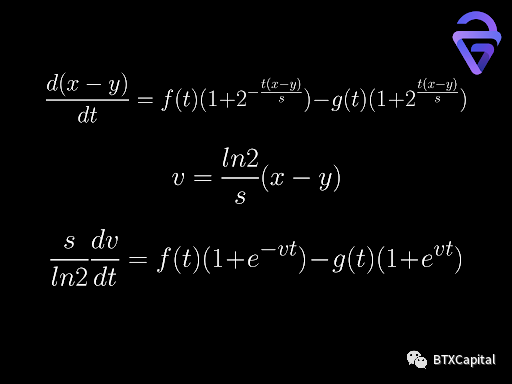
做市商函數有兩種形式,這兩種形式都會導出目前我們不知道如何求解的微分方程。在第二種形式的情況下,微分方程可以簡化為單個微分方程。
結論和未來工作:
我們希望這篇綜合性的、介紹性的、學習筆記風格的論文能夠為對AMM 算法一無所知的人和有更多經驗的人提供一些見解。
總而言之,AMM 算法的核心基本上是關於做市商函數的設計及其曲率分佈的操縱。顯然,我們需要閱讀另一篇
Guillermo Angeris 和Tarun Chitra 寫的論文¹⁷
,其中詳細討論了這一點。除此之外,還有高效的價格解決方案(如DEX 聚合器)和高效的流動性提供解決方案(如價格範圍)。最近的TWAMM 算法闡明了我們如何使用AMM 算法來實現中心化交易中常見的訂單簿類型的撮合。我們相信AMM 算法的未來將更接近訂單簿風格。
Guillermo Angeris 和Tarun Chitra 寫的論文¹⁷:Improved Price Oracles: Constant Function Market Makershttps://arxiv.org/abs/2003.10001
至於未來的工作,我們計劃對本文中提到的一些問題進行更深入的挖掘。這包括閱讀論文[4]、[5]、[7]、[16]、[17],推導其他AMM 的無常損失公式,推導其他AMM 的流動性分佈,了解模糊測試的工作原理,回答我們提出的關於Xcp 的3個問題,更多地了解如何選擇最有效的價格預言機和s 值,製作Curve 價格重錨過程的動畫,了解更多關於單邊流動性的創新,嘗試設計更好的動態權重K,將價格範圍應用於其他AMM,將TWAMM 應用到其他AMM 並找到更多解析解。
作者感謝Fangyuan Zhao、Showen Peng、DW 對本文研究課題提出十分有用的意見。作者還要感謝火幣研究院的Lianxuan Li。作者特別感謝Paradigm 的Dave White 和Dan Robinson 邀請加入TWAMM 討論組以及他們富有洞察力的討論。同時也要感謝BTX Capital的Vanessa Cao 和Jane Hu 對本文的翻譯和排版。
原文鏈接:https://link.medium.com/ynEydZUihjb

















