前言
在去年6 月份,我設想了用多因子模型去擇幣的簡單構思。
一年後,我們已經著手研發針對加密資產市場的多因子策略,並把整體的策略框架寫成系列的文章《用多因子策略建立強大的加密資產投資組合》。
一、「因子」是什麼
「因子」即技術分析中的「指標」、人工智慧機器學習的「特徵」,是決定加密貨幣殖利率漲跌的原因。
我們團隊把加密貨幣領域常見的因子類型:基本面因子、鏈上因子、量價因子、衍生性商品因子、另類因子和宏觀因子。
挖掘和計算“因子”的最終目的是為了準確計算資產的預期收益率。
二、「因子」的計算
(1)多因子模型的推導
起源:單因子模型—CAPM
因子研究可追溯於20C60S,資本資產定價模型(Capital Asset Pricing Model, CAPM)問世,該模型量化了風險如何影響一家公司的資本成本從而影響預期收益率。根據CAPM 理論,單一資產的預期超額報酬可由以下的一元線性模型決定:
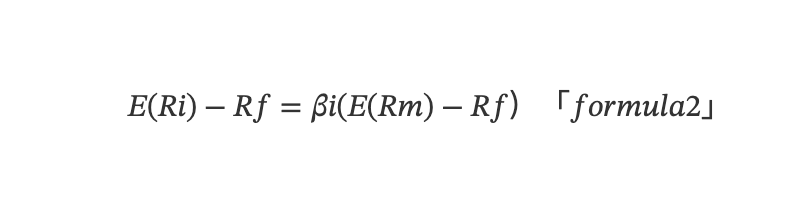
E(Ri)是數學期望,Ri為資產的收益率,Rf 為無風險收益率,Rm 為市場組合的收益率,βi = Cov(Ri,Rm)/Var(Rm) 體現資產收益對市場收益的敏感程度,也稱資產對市場風險的暴露程度。
補充理解:
金融市場中,所談及的「風險」和「收益」本質是同類東西。
從統計角度,更詳細的理解βi
CAPM 可看成是無截距項的雙變量迴歸模型Yi = β1 + β2 · X (β1 = 0),利用普通最小平方法估計法(OLS)求模型參數的估計值,其中β1 = β2 = Σ(X-μX)(Y-μY)/ Σ(X-μX)² = Cov(X,Y)/Var(X) 。
β1 衡量解釋變數(市場報酬率)變動以單位,被解釋變數(資產i 的報酬率)平均變動的程度,金融領域將變動程度解釋為Y 對X 的「敏感」或「暴露」程度。
β>1 放大市場波動
β = 1 與市場波動完全相同
0<β<1 與市場同向波動,但比市場波動小
β≤ 0 與市場反向波動
1.從金融學風險和利益的角度,更詳細的理解βi
投資組合有兩類風險,系統性風險(即市場風險、不可抵銷風險)及非系統性風險(可抵銷風險)。 βi 是系統性風險,無論如何建構資產組合,此風險是此系統特有的,無法抵銷。下文提及的αi 則是非系統性風險,可透過建構不同的策略來對沖掉。
CAPM 模型是最簡單的線性因子模型,指出資產的超額報酬只由市場組合(市場因子)的預期超額報酬和資產對市場風險的暴露大小決定。此模型為後續大量線性多因子定價模型的研究奠定基理論基礎。
發展:多因子模型—APT
在CAPM 基礎,人們發現不同資產的收益率受多個因子影響,套利定價理論(Arbitrage Pricing Theory, APT)問世,建構線性多因子模型:
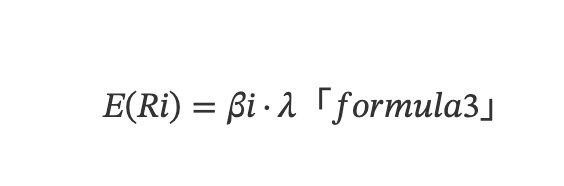
其中,E(Ri) 表示資產i 的預期收益,λ表示因子預期收益(即因子溢價)。公式(2) 利用E(Ri)代替CAPM 模型中的E(Ri) - Rf 來表示預期收益,利用多空對沖構建的資金中性投資組合資產,Rf 被抵消,整個資產的預期收益率就是多頭和空頭預期收益率之差,因此用E(Ri) 表示更具一般性。
成熟:多因子模型—Alpha 收益& Beta 收益
綜合考慮金融市場實際存在的定價誤差和APT 模型,從時序角度來看,單一資產的預期報酬率由以下的多元線性模型決定:
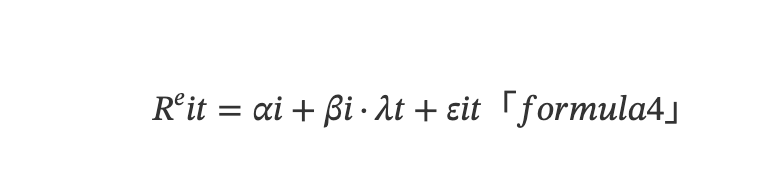
其中,Rᵉit 表示t 時刻資產i 的收益,λt 表示t 時刻因子收益率(即因子溢價),εit 表示t 時刻的隨機擾動。 αi 表示資產i 的實際預期報酬率和多因子模型隱含的預期報酬率之間的定價誤差,若統計上顯著偏離零,則代表了獲得超額報酬的機會。 βi = Cov(Ri,λ)/Var(λ) 表示資產i 的因素暴露或因子負荷,刻畫了資產收益對因子收益的敏感度。
多因子模型著重於資產預期報酬率在橫斷面上的差異,本質是關於平均值的模型,而預期報酬率是報酬率在時間序列上的平均。基於(3) ,可推導出截面角度的多元線性模型:
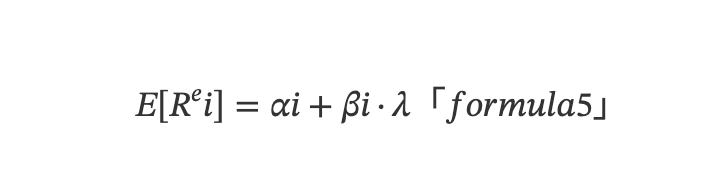
其中,E[Rᵉi] 表示資產i 的預期超額收益,εit 在時序上取平均,則E(εit)=0。
補充理解:
從學術界角度出發,根據市場有效性理論,一個有效的資產組合應該是可抵銷風險完全為0,實際收益率等於預期收益率,且預期資產收益率只取決於市場的系統性風險,即E [Rᵉi] = βi · λ,不存在超額報酬率(Abnormal Return, AR),即AR = Ri - E(Rᵉi) = 0。但現實的金融世界通常是市場非有效的,存在超額報酬率,即AR = α。
假設投資組合由N 資產構成,並將每個資產i 應的因子收益λ 依照不同因子展開,得到以下多因子模型的組合報酬率:
Rp = ∑ᴺᵢ₌₁Wi(αi+∑ᴹⱼ₌₁βᵢⱼfᵢⱼ)
其中,Rp 為組合的超額收益,Wi 是每份資產佔組合的權重,βij 是每份資產在每個因子上的風險暴露,λ = ∑ᴹⱼ₌₁βᵢⱼfᵢⱼ\),fᵢⱼ 是每份資產的每個因子每單位因子負荷對應的因子收益率。
結合統計學知識,此模型隱含三層假設:
每個資產的Beta收益和Alpha 收益不相關:Cov(αi,βiλ)=0
不同資產間的特質報酬率也不相關:Cov(αi,αj)=0
因子一定跟資產報酬率有關:Cov(Rᵉi,βiλ)≠0
對於Beta 收益和Alpha 收益的綜合解釋:
結合具體的金融市場,βiλ 是歸屬於大盤整體表現的Beta 收益,αi 則是由資產自身特定帶來的Alpha 收益,即跑贏大盤多少個點。而每個資產的收益率則是由Beta 收益和Alpha 收益組成,人們可利用多因子模型中每個資產對應的αi 值來對每個資產打分或賦予權重,從而構造投資組合,並利用期貨對Beta 收益部分做空來對沖風險,從而獲得Alpha 收益。
(2)多因子模型的波動率
構造投資組合時需在組合的風險和收益間取平衡,需要將以上模型轉換為帶約束的規劃問題來求解。組合的風險即組合的波動率σ²p,以下對σ²p 進行推導。涉及組合建構的詳細分析則在「風險組合最佳化」部分闡述。
基於公式(3) 的矩陣表達式Rp = W(β ∧ + α),可得到組合的波動率:
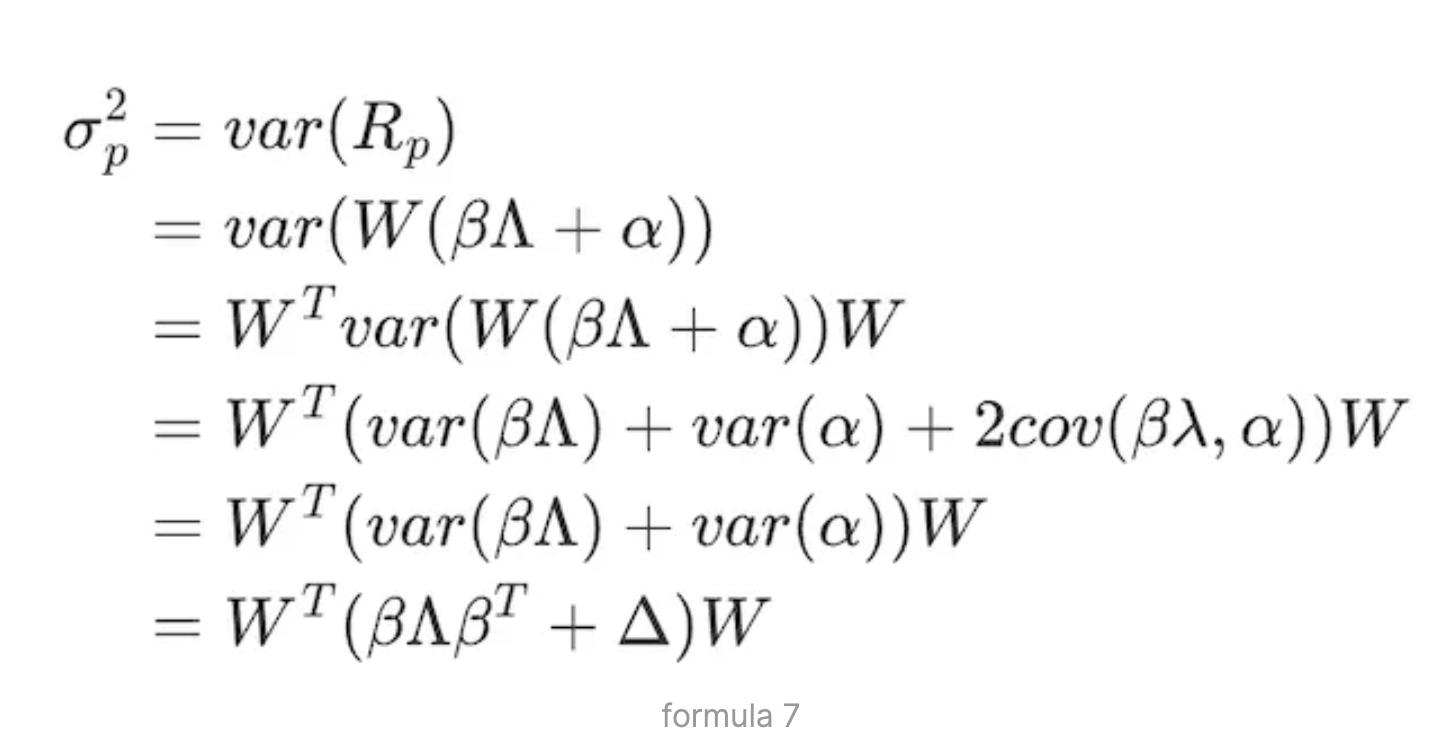
其中,W 是資產的權重矩陣,β是因子的權重矩陣,表示N 個資產在K 個風險因子上的因子負荷矩陣N×K:

∧表示K 個因子的因子報酬率協方差矩陣K×K :

由假設3,不同資產間的特質報酬率也不相關,可得Δ 矩陣為:


















