PART4.Modelling

協整
實際上,很難找到一種具有均值回歸行為的可交易資產。股票的總體表現類似於GBM,因此,均值回歸交易策略相對無用。然而,沒有什麼能阻止我們創建一個平穩的價格序列投資組合。因此,我們可以將均值回歸交易策略應用於投資組合。
均值回歸交易策略的最簡單形式是經典的“配對交易”,通常涉及美元中性的多/空股票對。該理論認為,同一行業的兩家公司很可能受到影響其業務的類似市場因素的影響。偶爾,它們的相對股價會因某些事件而出現背離,但會回歸長期均值。
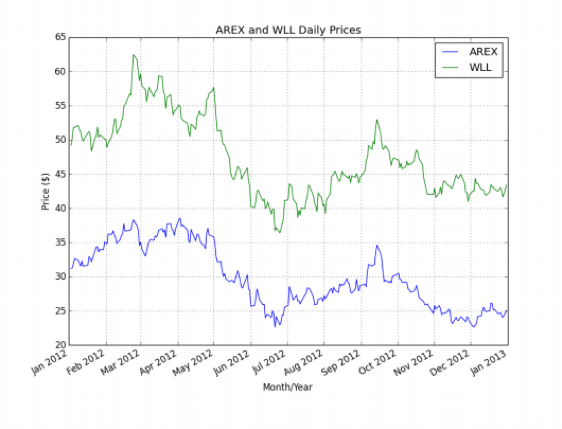
讓我們考慮兩家能源股公司,分別是股票代碼為AREX的資源公司(Resources Inc)和股票代碼為WLL的惠廷石油公司(Whiting Petroleum Corp)。兩者都處於相似的市場環境中,因此很可能存在平穩的配對關係。現在我們將創建一些圖形,使用pandas和Matplotlib庫來演示AREX和WLL的協整特性。第一個圖(圖10.1)顯示了2012年1月1日至2013年1月1日期間它們各自的價格歷史。
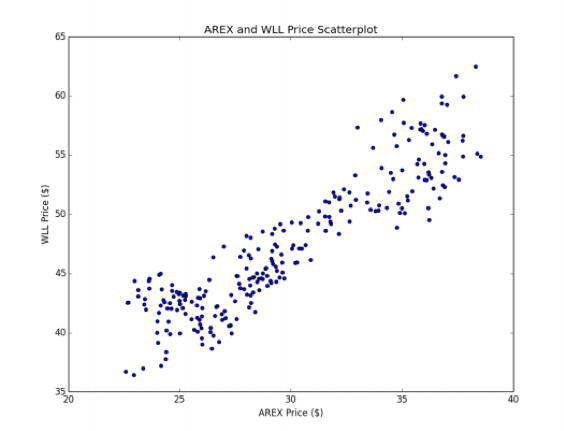
如果我們創建它們價格的散點圖,我們可以看到這段時期的關係大致是線性的(見圖10.2)。這組股票的交易本質上是通過一個線性模型來處理兩種股票價格之間的關係:

其中y(t)是AREX股票的價格,x(t)是WLL股票的價格,都在第t天。
如果我們畫出殘差 (為特定值的β將在下方決定)我們創建一個新的時間序列,乍一看,看起來相對固定。這在圖10.3中給出。
我們將在下面描述每個圖的代碼。

協整增廣Dickey-Fuller檢驗-為了在統計上確認這個級數是否均值回歸,我們可以使用上面描述的其中一個測試,即增廣的Dickey-Fuller測試或Hurst指數。然而,這些測試會幫助我們確定β,套期保值比率需要形成線性組合,他們只會告訴我們關於一個特定β,線性組合是否穩定。
這就是協整增廣Dickey-Fuller (CADF)測試的作用。通過對兩個時間序列進行線性回歸,確定最優套期保值比率,並對線性組合下的平穩性進行檢驗。
Python實現-現在,我們將使用Python庫測試AREX和WLL之間在2012年1月1日到2013年1月1日期間的協整關係。我們將使用Yahoo Finance作為數據源和statsmodel進行ADF測試,如上所述。
第一個任務是創建一個新文件cadf。 ,並導入必要的庫。該代碼使用了NumPy、Matplotlib、panda和statsmodel。為了正確標記坐標軸並通過panda從Yahoo Finance下載數據,我們導入了matplotlib。日期模塊和http:// pandas.io 。數據模塊。我們還利用了pandas的普通最小二乘(OLS)函數:
#!/usr/bin/python # -*- coding: utf-8 -*- # cadf.py import datetime import numpy as np import matplotlib.pyplot as plt import matplotlib.dates as mdates import pandas as pd import pandas.io.data as web import pprint import statsmodels.tsa.stattools as ts from pandas.stats.api import ols 第一個函數plot_price_series接受pandas Dataframe作為輸入,其列由佔位符字符串“ts1”和“ts2”給出。這些將是我們的配對股票。該函數簡單地將兩個價格序列繪製在同一個圖表上。這使我們可以直觀地檢查是否可能進行任何協整。
我們使用Matplotlib date模塊從datetime對象獲取月份。然後我們創建一個圖形和一組軸,用於應用標籤/繪圖。最後,繪製圖:
# cadf.py def plot_price_series(df, ts1, ts2): months = mdates.MonthLocator() # every month fig, ax = plt.subplots() ax.plot(df.index, df[ts1], label=ts1)94 ax.plot(df.index, df[ts2], label=ts2) ax.xaxis.set_major_locator(months) ax.xaxis.set_major_formatter(mdates.DateFormatter('%b %Y')) ax.set_xlim(datetime.datetime(2012, 1, 1), datetime.datetime(2013, 1, 1)) ax.grid(True) fig.autofmt_xdate() plt.xlabel('Month/Year') plt.ylabel('Price ($)') plt.title('%s and %s Daily Prices' % (ts1, ts2)) plt.legend() plt.show() 第二個函數plot_scatter_series繪製了兩個價格的散點圖。這讓我們可以直觀地檢查兩個系列之間是否存在線性關係,從而判斷它是否適合OLS過程和隨後的ADF測試:
# cadf.py def plot_scatter_series(df, ts1, ts2): plt.xlabel('%s Price ($)' % ts1) plt.ylabel('%s Price ($)' % ts2) plt.title('%s and %s Price Scatterplot' % (ts1, ts2)) plt.scatter(df[ts1], df[ts2]) plt.show() 第三個函數plot_residuals用於繪製兩個價格序列的擬合線性模型的殘差值。該函數要求panda DataFrame有一個“res”列,表示剩餘價格:
# cadf.py def plot_residuals(df): months = mdates.MonthLocator() # every month fig, ax = plt.subplots() ax.plot(df.index, df["res"], label="Residuals") ax.xaxis.set_major_locator(months) ax.xaxis.set_major_formatter(mdates.DateFormatter('%b %Y')) ax.set_xlim(datetime.datetime(2012, 1, 1), datetime.datetime(2013, 1, 1)) ax.grid(True) fig.autofmt_xdate() plt.xlabel('Month/Year') plt.ylabel('Price ($)') plt.title('Residual Plot') plt.legend() plt.plot(df["res"]) plt.show() 最後,該過程被封裝在一個__main__函數中。第一個任務是從Yahoo Finance下載AREX和WLL的OHLCV數據。然後,我們創建一個單獨的DataFrame df,使用與AREX框架相同的索引來存儲這兩個調整後的收盤價。然後繪製價格序列和散點圖。
繪圖完成後,通過調用WLL和AREX系列上的pandas ols函數計算殘差。這使我們能夠計算β對沖比率。然後,通過形成WLL和AREX的線性組合,利用對沖比率創建一個“res”列。
最後繪製殘差圖,並對計算出的殘差進行ADF檢驗。然後打印ADF測試結果:
# cadf.py if __name__ == "__main__": start = datetime.datetime(2012, 1, 1) end = datetime.datetime(2013, 1, 1) arex = web.DataReader("AREX", "yahoo", start, end) wll = web.DataReader("WLL", "yahoo", start, end) df = pd.DataFrame(index=arex.index) df["AREX"] = arex["Adj Close"] df["WLL"] = wll["Adj Close"] # 绘制两个时间序列plot_price_series(df, "AREX", "WLL") # 显示两个时间序列的散点图plot_scatter_series(df, "AREX", "WLL") # 计算最优对冲比率“贝塔” res = ols(y=df['WLL'], x=df["AREX"]) beta_hr = res.beta.x # Calculate the residuals of the linear combination df["res"] = df["WLL"] - beta_hr*df["AREX"] # 计算线性组合的残差plot_residuals(df) # 计算并输出残差的CADF测试cadf = ts.adfuller(df["res"]) pprint.pprint(cadf) 代碼的輸出如下:
(-2.9607012342275936, 0.038730981052330332, 0, 249, {'1%': -3.4568881317725864, '10%': -2.5729936189738876, '5%': -2.8732185133016057}, 601.96849256295991) 可以看出,-2.96的計算檢驗統計量小於-2.87的5%臨界值,這意味著我們可以拒絕在5%水平上不存在協整關係的原假設。因此,我們可以合理肯定地得出AREX和WLL至少在考慮的時間段樣本上具有協整關係。
我們將在後面的章節中使用這對組合來創建一個實際的交易策略,使用一個實現的事件驅動的回溯測試系統。
更多內容請關注公眾號【火象】~










