注3.6:如果啟動設置所計算的 [s],[s^2]…[s^d] 只計算到了指數d,這一組值是不能用來生成任何階數大於d 的多項式的承諾的。反之亦然。
因為在安全的曲線上,沒有辦法用兩個點相乘來得出第三個點,所以[s^(d+k)] 是一個(永遠!)無法求出的值,因此可以說,任意的承諾c(f) 都只能表示一個階數小於等於d 的多項式。
注3.7:使用KZG10 承諾的證據基本上就是在證明f(x) - 某些餘數的結果可以按特定的辦法來分解,但這就要有一種辦法可以相乘這些因數,並與原始的承諾相比較C(f)=f([s])。
為此,我們需要“配對方程”,就是一種能把曲線上的兩個點相乘並與另一個曲線點比較的乘法,因為我們無法直接讓這兩個曲線點直接相乘來得到合成的曲線點。
注3.8:上述兩個屬性,可以進一步用來證明某個承諾c(f) 所代表的多項式f(x) 的階數k 小於d。
綜上,KZG10 承諾可以有很好的屬性:
驗證承諾的過程是:(由區塊生成者)提供底層多項式在任意點r 上的值y=f(r) ,以及除法多項式q(x)=(f(x)-y)/(xr)在[s] 點的值(即q([s])),並用配對方程來對比之前所提供的承諾f[s]。這就叫 開啟 在r 點的承諾,而 q([s]) 就是證據。容易看出,q(s) 就是p(s)-r 除以sr ,恰好就是我們用配對方程來檢查的東西,即檢查(f([s])-[y]) * [1]'= q([s]) * [sr]' (譯者註:此處疑為f(s)-r ,但原文就是p(s)-r)。在非交互且確定性的版本中, Fiat Shamir Heuristic 提供了一種辦法來獲得相對隨機的點r:因為隨機性只跟我們嘗試證明的輸入有關,即,只要已經有了承諾c=f([ s]) ,r 就可以用哈希所有輸入(r=Hash(C,..))來獲得,而承諾的提出者要負責提供開啟點和證據。使用預先計算好的拉格朗日多項式,f([s]) 和 q([s]) 都可以在 求值形式 下直接計算。要計算r 處的開啟值,就需要把f(x) 轉為 f(x)=a0+ a1*x^1.... 的係數形式(也即抽取出 a0、a1、…)。可以通過反向快速傅立葉變換來實現,複雜度為O(d log d),但甚至這裡也有一種可用的替代算法,在O(d) 的複雜度內完成計算,而無需使用反向快速傅立葉變換。你可以使用單個開啟點和證據來證明f(x) 的多個值,也就是多個索引值對應的數值, index1=>value1、index2=>value2 …(用於計算證據的)除法多項式q( x) 現在變成了f(x) 除以零多項式z(x) =(xw^index1)*(xw^index2)...(xw^indexk) 的商餘數為r(x) ( r(x ) 是一個最大階數為k 的多項式,由index1=>value1, index2=>value2 … indexk=valuek 插值而成)檢查( f([s])-r([s]) )* [1] ' = q([s]) * z([s]')
在PoS 鏈的共同起步設置中,共享的數據塊會被表示為低階的多項式(並為了糾刪碼而使用同樣的擬合多項式擴展為兩倍大),KZG 承諾可以用來檢查任意隨機分塊並驗證和確保數據可得性,而無需獲得兄弟數據點。這就開啟了隨機取樣的可能性。
現在,對於一個最大可能包含2^28 個賬戶鍵的狀態,你需要至少2^28 階的多項式來構建 扁平的 承諾(flat commitment)(實際上的賬戶鍵總空間會大得多得多)。在更新和插入的時候,會有一些不便利。對任一賬戶的任意更改,都會觸發承諾(以及更麻煩的,見證數據/證據)的重新計算。
更新KZG10 承諾
對任一 索引值=> 數值 點的任何更改,比如更改了 indexk,都需要使用相應的拉格朗日多項式來更新承諾。複雜度約為每次更新 O(1)。但是,因為f(x) 本身也改變了,所以所有的見證 q_i([s]) ,也即所有對第i 個鍵值對的見證,也需要更新。總複雜度約為O(N)如果我們沒有維護預先計算好的q_i([s]) 見證,任何一條見證數據都要從頭開始計算,都需要O(N)一種複雜度為sqrt(N)的更新KZG10 承諾的構造
因此,為了實現理想承諾方案的第四點,我們需要一個特殊的構造:Verkle trie。 Verkle 樹需要表示的以太坊的狀態大約有2^28 約等於16^7 約等於2.5 億個鍵值對。如果我們只使用扁平的承諾(那麼我們需要的階數就至少是2^28)。雖然我們的證據永遠是48 個字節的橢圓曲線元素,但任意的插入或更新,都需要O(N) 次操作來更新所有預先計算好的見證數據(也就是所有點的q_i(s) ,因為f(x) 本身已經改變了);甚至於,如果沒有預先計算好的見證數據,則每條見證數據都需要花O(N) 來重新計算。
因此,我們需要把扁平的結構換成叫做 Verkle 樹 的結構,跟默克爾樹一樣是樹結構。
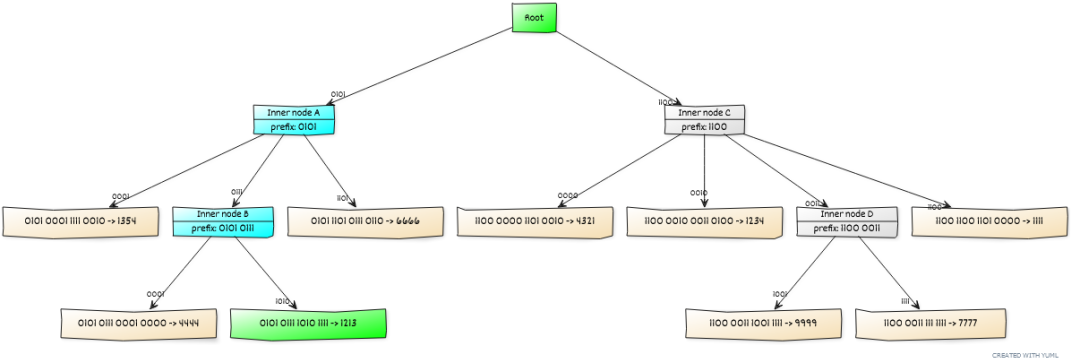
即,像默克爾樹一樣,構建出一棵承諾樹,這樣我們就可以保證階數d 比較小(但也需要高達約256 或者1024)。
每個父節點都編碼對其子節點的承諾,子節點就是一個映射,其索引值都存在其父節點內實際上,父節點的承諾編碼了哈希後的子節點,因為承諾的輸入是標準化的、32 字節的值(見上文的注3.0)。葉子節點編碼了對其所存儲的數據的32 字節哈希值的承諾;或者直接跳轉到數據,假如其32 字節的數據的用法與下一章提到的 狀態樹 提議用法一樣的話。要提供對一個分支的證據(類似於默克爾分支證據)時,一個多值證明的承諾 D、E 可以圍繞使用fiat shamir heruristic 產生一個相對隨機的點t 來生成。
複雜度這裡是一份對Verkle 多值證明的分析更新/插入葉子節點index=>value 需要更新log_d(N) 個承諾~ log_d(N)為生成證據,證明者需要計算f_i(X)/(X -z_i) 在[s] 處的值,用於生成D ,複雜度總計O(d log_d N),但可以在更新/插入時調整以節約預計算,複雜度會變成O d log_d(N)計算m 個~ O( log_d(N) ) 個f_i(t) 來計算h(t),總計為O (d log_d N)計算π, ρ ,需要對m~ log_d N 個指數多項式的和做除法。需要約 O(d log_d N) 來獲得分子的求值形式,以計算除法證明的規模(包括用於計算 E 的分支承諾)加上驗證的複雜度~ O( log_d(N) )
Verkle 樹構建
被提議的ETH 狀態Verkle 樹單一的樹結構,存儲賬戶的 header 和 代碼分塊,還有 存儲項分塊,節點的承諾為階數d=256 的多項式
把地址和頭/存儲空檔結合起來推導出一個32 字節的storageKey,本質上就是元組(address,sub_key,leaf_key) 的一種表示所推導的鍵的前30 個字節用於構建普通的verkle 樹節點pivots後2 個字節是一個樹高為2 的子樹,表示最多65536 個32 字節的分塊對於基本的數據,這個樹高為2 的子樹最多有4 個葉子承諾,來覆蓋haeader 和code因為一個分塊為65536*32 字節的分塊表示為單個的字數,所以主樹上可能有許多子樹來存儲一個賬戶Gas 定價方案訪問類型(address, sub_key, leaf_key) 的事件每一個專門的訪問事件都收取WITNESS_CHUNK_COST每個專門的address,sub_key 組合都收取額外的WITNESS_BRANCH_COST
代碼默克爾化
代碼會自動成為verkle 樹的一部分(作為統一的狀態樹的一部分)
一個區塊的header 和code 都作為一個樹高為2 的承諾樹的一部分單個分塊最多有4 條見證數據,分別收取 WITNESS_CHUNK_COST,訪問賬戶需要收取一次 WITNESS_BRANCH_COST
數據採樣和PoS 協議中的分片
ETH PoS 的目標之一是能夠提交約1.5MB/s 的數據量(把這個吞吐量理解為狀態變更的吞吐量,因而是L2 rollup 可以利用的交易吞吐量,最終是L1 EVM 的吞吐量)。要實現這一點,許多並行的區塊提議要能發出並在給定的12 秒內驗證;也就是要存在多條分片(約64),每個分片在每個slot 都要發布自己的數據塊。若有大於2/3 的投票支持,信標鏈區塊將包含分片數據塊,分叉選擇規則也將根據信標鏈區塊內所有數據塊及其祖先的數據可得性確定它是否能成為主鏈區塊。
注3:此時的分片不是鏈,任何隱含的順序都要由L2 協議來解釋。
KZG 承諾也可以用來構建
數據有效性和可得性方案,客戶端無需訪問分片提議者發布的完整數據就可以校驗其可得性。
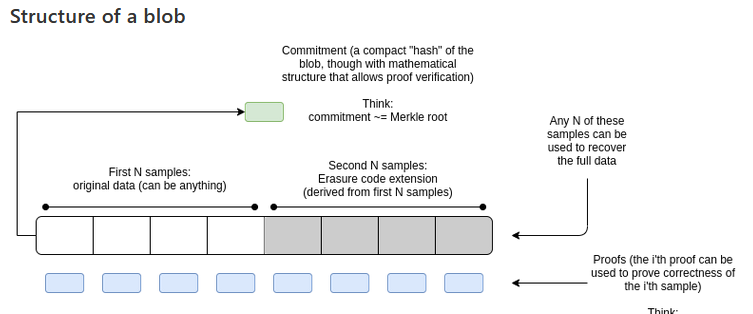
分片數據塊(不帶糾刪碼)是16384 個樣本(每個32 字節),約為512 kb;還有數據頭,主要由這些樣本相應的最大16384 階的多項式承諾組成但多項式求值形式D 卻有2^16384 的規模,即,1,w^1,…w^,… w^32767,而W 是32768 的單元根(不是16384 的)我們可以為數據(f(w^i) =sample-i for i<16384)擬合出最大16384 階的多項式,並擴展到32768 作為糾刪碼樣本,即計算f(w^16384) … f(w^32767)對每個點的值的證明也同時計算並與樣本一起發布32768 個樣本中獲得任意16384 個都可以完全恢復出f(x) 以及原始的樣本,即f(1),f(w^1),f(w^2) … f(w^16383)這糾刪編碼的32768 個樣本分為2048 個分塊,每個分塊包含16 個樣本,即512 字節的數據;由分片提議者水平地發布,即將第i個分塊以及相應地證據發給第i 個垂直子網絡,外加全局公開完整數據的承諾在被指定的(shard, slot),每個驗證者都在k~20 個垂直子網中下載和檢查這些分塊,並使用對應數據塊的承諾來驗證它們,以建立數據可得性保證我們需要為每個(shard, slot) 安排足夠多的驗證者,使得總體上一般(乃至更多的數據)都被獲取了;另外,還要滿足一些統計學上的要求,每個(shard, slot) 約128 個委員,需要有至少70 個(也即2/3 )委員的見證,使得該分片數據塊能成功打包到信標鏈上,至少需要約262144 個驗證者(32 個slot,乘以64 個分片,再乘上至少128 個委員)
基準測試
如我們在POC verkle go 代碼庫中看到的,以狀態樹的規模構建完一次verkle 之後,插入和更新都非常快:
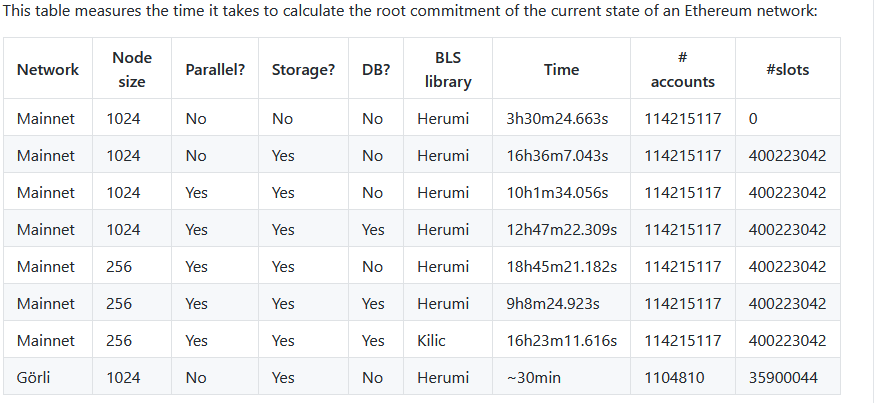
插入/更新的基準測試
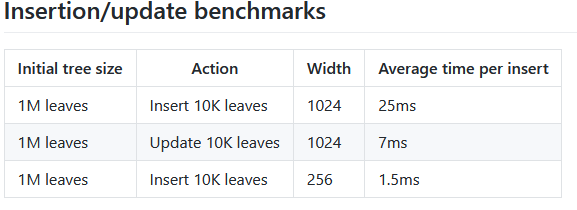
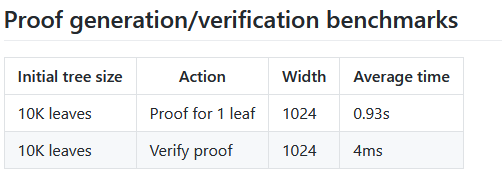
證明生成驗證的基準測試
(完)
(文內有許多超鏈接,可點擊左下”閱讀原文“ 從EthFans 網站上獲取)
原文鏈接:https://hackmd.io/yqfI6OPlRZizv9yPaD-8IQ
作者: g11tech
翻譯: 阿劍











