本文旨在簡單介紹橢圓曲線密碼學(elliptic curve cryptography)。本文預設讀者的閱讀目的是想知道為什麼ECC 是一個有效的密碼學工具及其基本原理。我的目標是給出廣義的解釋,我將省略一些證明和實現細節,聚焦於抽象的原理。
- 橢圓曲線示例-
ECC 有什麼用途?
ECC 是一種加密數據的方法,只有特定的人才能對其進行解密。在現實生活中,ECC 有一些常見的用例,但是最主要的用途是加密互聯網數據和流量。例如,ECC 可以用來確保在發送電子郵件時,除收件人以外沒人可以閱讀郵件內容。
ECC 是一種公鑰密碼學
公鑰密碼學的類型有很多,ECC 只是其中一種。此外還有RSA、Diffie-Helman 等算法。首先,我要簡單介紹一下公鑰密碼學的背景,然後再討論ECC 以及這些概念基礎上的高層建築。請各位讀者在有空時深入學習一下關於公鑰密碼學的知識。
公鑰密碼學的運作方式如下圖所示:
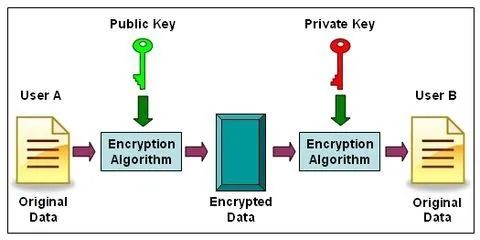
- Wikia.org -
上圖顯示了兩個密鑰:公鑰和私鑰。這兩個密鑰分別用來加密和解密數據。這樣一來,加密數據在傳輸的過程中,全世界的人都可以看到(密文),卻無法知道其內容。
假設Facebook 將要收到來自特朗普的私信。 Facebook 需要確保特朗普在通過互聯網發送私信時,沒有中間方(國家安全局、互聯網服務提供商)能夠讀取該私信。在使用公鑰密碼學的情況下,整個過程如下:
特朗普通知Facebook 說他想發送一封私信給FacebookFacebook 將自己的公鑰發送給了特朗普特朗普使用該公鑰加密了私信:“I love Fox and Friends” + Public Key = “s80s1s9sadjds9s”特朗普將加密後的私信發送給FacebookFacebook 使用私鑰解密該私信“s80s1s9sadjds9s” + Private Key = “I love Fox and Friends”
如你所見,公鑰密碼學是一個非常有用的技術。以下是一些關鍵點。
公鑰可以發送給任何人,它是公開的。必須保護好私鑰。如果中間方獲得私鑰,他們就能解密私信。計算機可以使用公鑰快速加密消息,使用私鑰快速解密消息。如果沒有私鑰,計算機需要很長一段時間(數百萬年)才能暴力破解加密消息。
公鑰密碼學原理:陷門函數
對於所有公鑰密碼學算法來說,最關鍵的是它們都有自己獨特的陷門函數(Trapdoor Function)。陷門函數是一種只能單向計算,至少是只在一個方向上易於計算的函數。 (如果使用現代計算機從另一個方向暴力破解,需要數百萬年時間。)
非陷門函數的例子:A + B = C
已知A 和B,我就能計算出C 。問題在於,在已知B 和C 的情況下,我也能計算出A 。這就是非陷門函數。
陷門函數:
“I love Fox and Friends” + Public Key = “s80s1s9sadjds9s”
已知“I love Fox and Friends” 和公鑰,我可以計算出“s80s1s9sadjds9s” ,但是已知“s80s1s9sadjds9s” 和公鑰,我無法計算出“I love Fox and Friends” 。
在RSA 算法(可能是最受歡迎的公鑰系統)中,陷門函數取決於將一個巨大的數分解成質因數的難易程度。
公鑰:944,871,836,856,449,473 私鑰:961,748,941 和982,451,653
在上述例子中,公鑰是一個很大的數,私鑰是公鑰的兩個質因數。這是一個很好的例子,因為將私鑰中的數相乘,很容易就能算出公鑰,但是你只有公鑰的話,需要很長時間才能使用計算機算出私鑰。
注:在真正的密碼學實踐中,私鑰的長度必須超過200 位才能被視為是安全的。
橢圓曲線密碼學有什麼不同?
ECC 與RSA 的用途相同。 ECC 會生成一個公鑰和私鑰,允許雙方安全通信。不過,ECC 相比RSA 有一大優勢。一個256 位的ECC 密鑰與一個3072 位的RSA 密鑰安全性相同。也就是說,在資源有限的系統(如智能手機、嵌入式計算機和加密貨幣網絡)中,ECC 密鑰需佔用的硬盤空間和帶寬是RSA 密鑰的10% 不到。
ECC 的陷門函數
重點來了。 ECC 與RSA 的主要區別在於陷門函數。 ECC 的陷門函數類似於數學版的台球遊戲。我們先在曲線上找到一個特定的點,然後使用函數(通常稱為點函數)在曲線上找到一個新的點,接著重複使用點函數,在曲線上不斷跳躍,直到找到最後一個點為止。我們來看一下該算法的具體步驟:
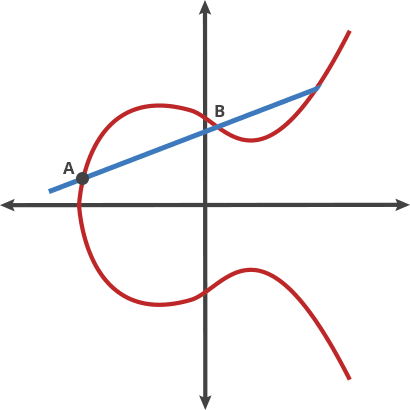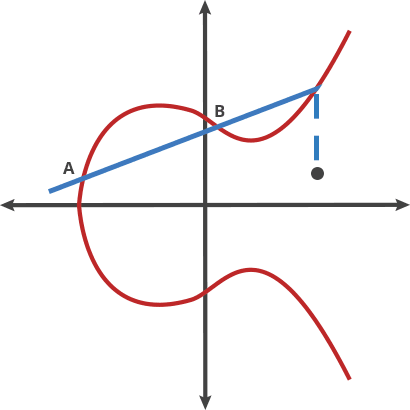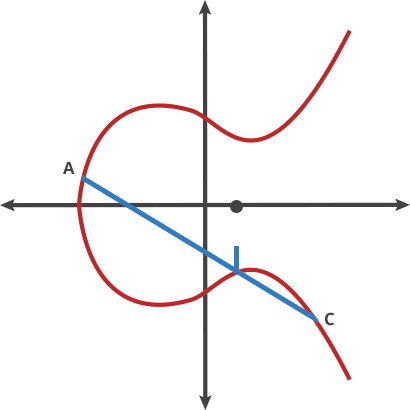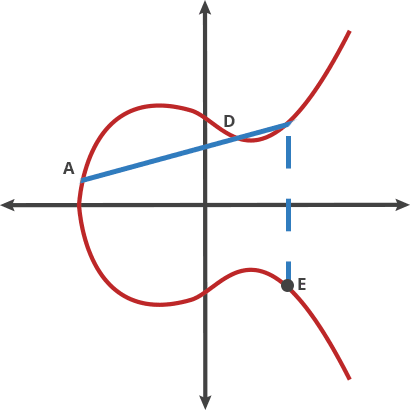
- arstechnica.com -
從A 點開始:A dot B = -C(從A 點至B 點畫一條直線,與曲線相交於-C 點)-C 點經過X 軸反射到曲線上的C 點A dot C = -D (從A 點至C 點畫一條直線,與曲線相交於-D 點)-D 點經過X 軸反射到曲線上的D 點A dot D = -E (在A 點至D 點畫一條直線,與曲線相交於- E 點)-E 點經過X 軸反射到曲線上的E 點
這是一個很棒的陷門函數,因為如果你知道起點(A)在哪裡,以及到達終點(E)需要經歷多少次跳躍,很容易就能找到終點。但是,如果你只知道起點A 和終點E 在哪裡,幾乎不可能知道中間經歷了幾次跳躍。
公鑰:起點A 、終點E 私鑰:從A 點至E 點需要經歷幾次跳躍
幾點疑問
以下是我初次學習ECC 時遇到的幾點疑問,以及我的解答。希望能給各位讀者帶來幫助。
如何找到第二個點?如果點函數主要依靠在兩個點之間畫一條直線,我們不需要知道第二個點在哪裡(就能開始計算)嗎?
回答:不需要,因為第二個點(假設是-R)實際上是P dot P(假設第一個點是P)得出的結果。
P dot P= -R
那什麼是P dot P?它實際上就是一條經過P 點的切線。參見下圖:
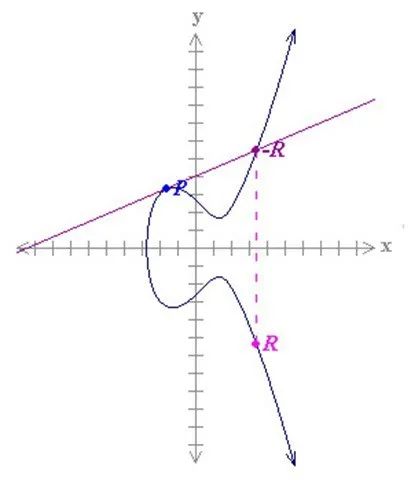
- f5.com -
如果點函數產生的直線與曲線的交點距離原點太遠,那該怎麼辦?
如果直線與曲線的交點距離原點太遠,我們可以定義一個最大值X 。如果超過X 值,直線就會繞回來,從Y 軸重新開始。如下圖所示:

- arstechnica.com -
我發現了一個陷門函數,如何創建公鑰和私鑰?如何用它們來加密數據?
這是一個很好的問題,但是需要更深入的解答。在本文中,我只想簡單解釋RSA 和ECC 。各位讀者可以查閱更多技術資料來了解具體細節。
(譯者註:雖然作者在原文中自述學習橢圓曲線密碼學是出於自己對比特幣和數字貨幣的興趣,但此處所講述的原理集中在加解密上,還未涉及橢圓曲線在數字貨幣(至少是以太坊)中的主要用途:驗證交易的權威性。在以太坊中,用戶發送交易的過程並不是使用公鑰或私鑰加密交易數據,而是使用私鑰對交易數據簽名,這些簽名信息隨交易發送,得到這些簽名信息的節點可使用橢圓曲線算法恢復出一個地址,與交易原始數據比對即可知該筆交易是不是由有權使用該地址的用戶發出的。)
(完)
原文鏈接:
https://blog.goodaudience.com/very-basic-elliptic-curve-cryptography-16c4f6c349ed
作者: Lane Wagner
翻譯&校對: 閔敏 &阿劍













